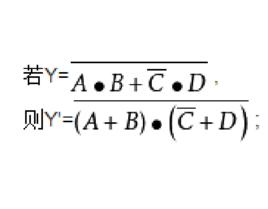定義
對偶定理是揭示原始問題的解與對偶問題的解之間重要關係的一系列定理。
(對偶定理) 設Y，y，γ以及S，s同前，如果存在可容許的向量p和ξ，則S和s都有限，並且S=s ．
舉例
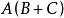對偶定理
對偶定理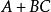若Y= ,則Y'= ;
對偶定理
對偶定理若Y= ,則Y'= ;
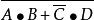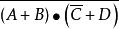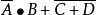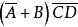對偶定理
對偶定理若Y= ,則Y'= .
若兩邏輯式相等，則它們的對偶式也相等，這就是對偶定理(Duality theorem)。
同一個電路，按正邏輯和負邏輯規定所得到的邏輯表達式不一定相等，也不一定相反，它們之間是對偶的關係。所以如果兩個電路在正邏輯下是相等的，那么在負邏輯下也必定是相等的，這就是對偶定理的實質 。
有時候直接證明兩個邏輯式相等比較麻煩，但其對偶式的證明比較簡單，可以先證明其對偶式相等，再利用對偶定理就得到原式相等 。
性質定理與推論
性質 對偶問題的對偶仍是原問題。
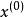對偶定理
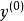對偶定理定理1 (弱對偶定理)如果 是原問題的可行解， 是對偶問題的可行解，則恆有
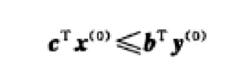對偶定理推論1 原問題任一可行解的目標函式值是其對偶問題目標函式值的下界；反之對偶問題任一可行解的目標函式值是其原問題目標函式值的上界。
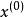對偶定理 對偶定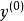理
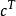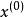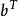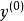對偶定理 對偶定理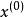
對偶定理 對偶定理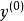 對偶定理 對偶定理定理2 (最優準則定理) 如果 是原問題的可行解， 是對偶問題的可行解，則當 = 時， 、 分別為各自問題的最優解。
定理3 (最優解存在定理) 若原問題和對偶問題同時存在可行解，則它們必都存在最優解。
證明：最大化問題LP的目標函式值有上界，所以一定有最優解，類似地，最小化問題
DP的目標函式值有下界，所以也一定有最優解。
證畢。
定理4 (無界解定理) 若原問題(或對偶問題)有可行解且目標函式值無界，則其對偶問題(或原問題)無可行解。
定理5 (強對偶性定理) 如果原問題和對偶問題中有一個有最優解，則另一個問題也必存在最優解，且兩個問題的最優解的目標函式值相等。
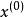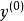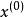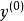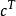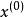對偶定理 對偶定理 對偶定理 對偶定理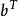 對偶定理 對偶定理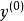 對偶定理 對偶定理推論2 設 ， 分別是對稱形式的原問題式和其對偶問題式的可行解，則 ， 分別是原問題和對偶問題的最優解的充分必要條件為 = .
推論3 若原問題式有最優解，則在其最優單純形表中，鬆弛變數的檢驗數的負值即為對偶問題的一個最優解。
定理6 (互補鬆弛性定理) (向量形式)設x，y分別是對稱形式的原問題式和其對偶問題式的可行解，則 x， y分別是原問題和對偶問題的最優解的充分必要條件為：
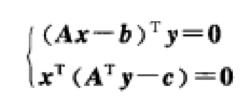對偶定理(分量形式)設 x=(x1，x2，…，xn)T， y=(y1，y2，…，yn)T分別是原問題式和其對偶問題式的可行解，則 x，y分別是原問題和對偶問題的最優解的充分必要條件為：
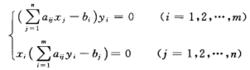對偶定理