定義
 反演定理
反演定理 反演定理
反演定理 反演定理
反演定理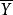 反演定理
反演定理反演定理是這樣表述的:對於任意一個邏輯式,如果把其中所有的“”換成“+”,“+”換成“”,0換成1,1換成0,原變數換成反變數,反變數換成原變數,得到的結果就是。
規則
在運用反演定理時還需注意遵守以下規則:
(1)仍需遵守“先括弧內,後括弧外,先乘後加”的運算順序;
(2)不屬於單個變數上的反號應保留不變。
用反演定理可以很方便地求出邏輯函式的反函式。
例題解析
 反演定理
反演定理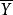 反演定理
反演定理例1 已知邏輯函式求。
解:根據反演定理可寫出:
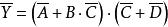 反演定理
反演定理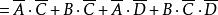 反演定理
反演定理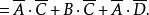 反演定理
反演定理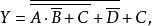 反演定理
反演定理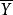 反演定理
反演定理例2 已知邏輯函式求。
解:根據反演定理可寫出:
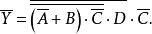 反演定理
反演定理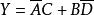 反演定理
反演定理例3 求函式的反函式。
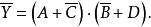 反演定理
反演定理解:
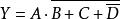 反演定理
反演定理例4 求函式的反函式。
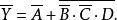 反演定理
反演定理解:
注意:
(1)要注意運算的優先順序(先括弧,然後乘,最後加),必要時加括弧,如例3。
(2)變換中,幾個變數(一個以上)的公共非號保持不變,如例4。