太極計算

百科名片

經典二進制計算機出現了運算極限，如何解決該極限問題是計算機科學界面臨的最大難題。太極是指能夠以自由狀態存在的最小的物質組成部分，它從數學角度看是其值為1的無差別的點、方格、球體或正立方體(點、方格、球體或正立方體在趨於無限小時視作無差別)。量子是由“太極”構成並具有相對一般穩定性的一個數學新概念。經典二進制計算機與我國古代的“太極”理論有著極大的關係，太極計算就是在我國古代“太極”理論的基礎上，直接利用太極生成的四象來實現計算機邏輯運算的一種新的數學理論，其目的就是要解決經典二進制計算機出現的運算極限問題。

太極計算的含義

太極計算就是將太極定義為其值為1的無差別的點、方格、球體或正立方體(點、方格、球體或正立方體在趨於無限小時視作無差別)後，引入計算機邏輯運算體系，以改善計算機運算性能的一種新的數學理論。

太極計算與數學危機

數學的最初研究對象只是簡單的計算問題，而是現代數學卻把研究對象演變成了“問題”本身，或者說如何運算“問題”才是現代數學的本質。之所以在首先就要探討數學的研究對象，是因為把這個問題搞清楚，羅素等數學家提出的悖論以及第三次數學危機就可化解。因為羅素等數學家提出的悖論以及第三次數學危機問題和“先有雞還是先有蛋”問題如出一轍，都不是“合理存在”，根本就不是數學問題，而是“非數學”問題。讓數學來回答“非數學”問題肯定不會有結果的。所以，對於經典邏輯來說,“悖論”和“危機”都是人為臆造的,“悖論”和“危機”只能算是人類邏輯的主觀障礙而已。但是，如果我們利用“太極圖”來觀察問題，能將“非數學問題”轉化成“數學問題”的時候，矛盾結論就會忽然之間協調統一起來。比如：我們先觀察“太極圖”中只包含一個電路比特情況。觀察後我們的結論是：計算機上運行的比特只能是0或1，肯定不存在半真不假的既是0又是1或者既不是0又不是1的數字。否則，現實世界就應該有薛丁格半死不活的貓或者羅素所指的既給給自己又不給自己刮臉的理髮師。接著我們再觀察“太極圖”中包含兩個電路比特的情況。觀察後我們的結論是：計算機上運行的比特既是0也不是0、既是1也不是1的數字，既可能是疊加態00或11，也可能是糾纏態01或10。如果把死貓和活貓、理髮師a和b同時放入兩個電路比特中的話，現實世界就會有半死不活的貓或者既給給自己又不給自己刮臉的理髮師。前後使用的兩種邏輯我們稱之為線性形式邏輯（以下稱作線邏輯)和面性量子邏輯（以下稱面邏輯）。在“太極圖”下，我們發現線邏輯和面邏輯發生矛盾的根源是觀察問題的方式和邏輯推理工具的不同。線邏輯使用的是0或1，在其運算過程中會出現“單一排斥”效應，所以不會承認：既是0也不是0或者既是1也不是1的數字存在。而面邏輯使用的是0和1，在其運算過程中會出現“多元相干”效應，所以不會承認：只能是0或1的數字存在。這兩種邏輯表面上看起來相互矛盾，實際上二者是相通的。就像正數和負數、實數和虛數一樣總會有一種數學理論將其同一起來。線邏輯和面邏輯的統一理論就是：太極計算理論。

太極計算機與量子計算機

線邏輯的運算基礎是二進制邏輯電路即“一元太極圖”，也就是說線邏輯是利用“一元太極圖”中單一對象0或1來實現運算，那么面邏輯的運算基礎應該是什麼？如果面邏輯能利用“太極圖”中多元對象00、01、10、11運算的話，“二元太極圖”不就變成了面邏輯的運算基礎了嗎？關鍵要看“二元太極圖”能不能搭建任意的邏輯線路（連續的“二元太極圖”串）以及實現任意邏輯運算。我們把基於邏輯電路二進制中使用的用0或1表示的電路比特和電路比特之間的關聯做虛擬掐斷，利用“二元太極圖”將兩個電路比特組合起來，形成的兩個電路比特組合體，稱之為“二元太極比特”（也叫量子比特）,再將“量子比特”組合起來形成的的組合體稱之為“二元太極位元組”（也叫邏輯量子）。有了量子比特和邏輯量子，就可利用“二元太極圖”生成任意邏輯線路；有了任意邏輯線路，邏輯量子即可在任意邏輯線路的基礎上完成任意邏輯運算，“二元太極圖”就變成了面邏輯的運算基礎。“邏輯量子”作為基本運算單元的處理器實際上是一個相對脫離了邏輯電路束縛的一個“量子運算中樞”，這個“量子運算中樞”就是為經典計算機增設的思維系統，也可理解為經典計算機的“大腦”。如果量子位至少是8位量子比特（並且不同於微軟雙位元組Unicode碼），該大腦至少使用有4^8=65536種“量子位元組”，65536種“量子位元組”足以描述全人類語言用字元，將全部人類語言用字元置入經典計算機底層後，經典計算機就變成了自然語言量子計算機。假想“圖靈機”的基本思想是用機器來模擬人們用紙筆進行數學運算的過程，自然語言太極計算機實際上就是計算機科學家夢寐以求的“非確定型圖靈機”。“非確定型圖靈機”的出現標誌著計算機的機器語言電路比特計算時代的終結，代之而起的將是計算機的自然語言太極計算（軟量子計算）時代的開始。雖然不能說經典二進制計算機是我國古代太極理論的產物，但二者的邏輯本質是統一的。目前很多國家或機構花費巨資研發的量子計算機是通過物理方法在計算機上實現量子運算，而太極計算機是通過數學方法在計算機上實現65537進制量子運算，所以太極計算機也叫軟量子計算機。

太極計算的數學套用

NP=P的太極證明

任何理論都是用來解決實際問題的。太極計算就是利用太極生成的四象來實現計算機邏輯運算而創立的一種數學理論，人類目前的最大邏輯問題是NP=P。如何利用太極計算理論來解決NP=P問題呢？P問題是可以在多項式時間內被確定機(經典計算機)解決的問題，實際上解決的就是線邏輯解決的運算問題，所以說，P=邏輯電路運算問題。NP問題是指可以在多項式時間內被非確定機(未來圖靈機)解決的問題，實際上解決的就是面邏輯的邏輯量子運算問題，所以說，NP=邏輯量子運算問題。所有NP問題用一句話總結就是：由於經典計算機上使用的二進制線邏輯運算能力的局限造成了運算時間過長使得經典計算機的運算沒有了實際意義的“某類問題”。或者說：未來圖靈機計算機解決的問題是否在經典經典計算機上得到驗證；再或者說：是否存在一種“魔法工具”能夠使得未來圖靈機解決的問題轉換成經典計算機解決的問題，如果是，則NP=P；如果不是，則NP≠P。那么魔法工具在哪裡呢?邏輯電路運算是一種二分樹結構運算，採用的是將所有可能性都“堵”在前方，逐步推算，最終給出結論。經典計算機的能力總歸有限，當“堵”在前方的問題的複雜度增加到一定程度成都後，會出現無力推算或在多項式時間內無法解決的問題，即NP問題。這時候，我們將“堵”改做“疏”（大禹治水的方法），二分樹結構運算改用太極計算結構運算後，問題會突然之間得到解決。太極計算結構將總體複雜度轉換成每一種可能性的獨立運算，可能性之間進行並行運算，最後將所有獨立運算的結果匯總整理後在多項式時間內給出最終結果。所謂魔法工具就是太極運算器。太極運算器的運算關鍵點是“同時”或“並行”，“同時”或“並行”運算為太極運算器贏得了時間，使得NP問題變成了P問題。比如旅行推銷員問題可以理解為如下：假設有n個城市，推銷員的推銷路徑有M種，如果同時派出M個推銷員通過M種路徑推銷，最先回到出發地的推銷員所經過的路徑就是在不同城市間的最短路徑。如果用太極運算器進行計算的話，就是用M個處理器同時、並行計算M種路徑的距離，然後在M種路徑中比較找出最短路徑。所以說旅行推銷員問題對於太極運算器來說就是P問題而不是NP問題。再比如：英國倫敦大學皇家霍洛韋學院等機構研究人員的報告中提出：小蜜蜂顯示出了輕而易舉破解NP=P問題的能力。太極計算分析如下：假設有n朵花，蜜蜂采蜜路徑有M種，同時派出M只蜜蜂通過M種路徑采蜜，最先回到出發地蜜蜂所經過的路徑就是采蜜的最短路徑。所以，不管人工怎樣改變花的位置，蜜蜂在稍加探索（同時派出M只蜜蜂通過M種路徑采蜜）後，最先回來的蜜蜂攜帶了最短路徑信息，也即蜜蜂很快就可以找到在不同花朵間飛行的最短路徑。

費爾馬大定理的太極證明

1637年，法國業餘大數學家費爾馬（Pierre de Fremat）在“算術”的關於勾股數問題的頁邊上，寫下猜想：x^n+ y^n =z^n 是不可能的（這裡n大於2；x，y，z，n都是非零整數)。一般公認，他當時不可能有正確的證明。其實不然，我們沿著費爾

馬的思路，首先用太極計算理論來證明勾股定理：首先建立一個太極圖（如右圖）。從太極計算角度看a^2是一個正方形（太極可以是無差別的點、方格、球體或正立方體），先將該正方形向左下兩邊搬移（當a是奇數時一個一個方格搬移，當a是偶數時兩個兩個方格搬移），形成兩邊等長並長為c的L形（如右圖紅色部分），再將b^2（如右圖藍色部分）對應的正方形補全，由於c^2（如右圖紅藍兩部分）是a^2和b^2緊密搬移而成，所以a^2+b^2=c^2，即勾股定理成立。繼續從太極計算角度看a^2、b^2、c^2是三個正方形，而a^3、b^3、c^3是三個正立方體。a^2+b^2=c^2成立時，a^3+b^3和c^3相比，是底面積相同高不同的幾何體，也可解釋為太極立方體數量不等的兩個幾何體，a^3+b^3數量<c^3數量，即a^3+b^3≠c^3。當n≧3的時候，a^n、b^n、c^n是太極立方體成倍向上壘砌而成的幾何體，a^n+b^n數量永遠小於c^n數量，故n≧3，a^n+b^n≠c^n，即費爾馬大定理成立。太極計算推導出的勾股擴展定理以及質數方程

在上述證明勾股定理的過程中使用的太極可以得出來一個關於整數的勾股擴展定理(勾股定理整數求解方程)：任何整數a的平方肯定是某一對相鄰數b和c（c>b）的平方差。當a為奇數時，b和c是兩個相鄰奇偶數，b是偶數，c奇數是（求某一奇數對應勾股值使用方程b=（a^2-1）/2,c=b+1）；當a為偶數時，b和c是兩個相鄰奇數或相鄰偶數（求某一偶數對應勾股值使用方程b=（a^2-4）/4,c=b+2）。有了勾股擴展定理，利用太極計算幾何原理和統計學原理很容易就可再獲得一個質數定理：當a≥7並為質數時，質數a為“勾”對應的“股”b能被6整除。也就是說存在這樣一個方程y=（x^2-1）/12，所有質數都是該方程中x的有意義整數解。這時候我們發現，所有質數都是該方程中x的有意義整數解，但該方程中x的所有有意義的整數解不一定是質數，所以我們引入一個新概念-泛質數：其股(勾股定理中和勾相對的股)能被6整除的奇數。泛質數包含強質數和弱質數；強質數就是通常意義的質數，即除1和自身外不能被任何數整除的整數；弱質數就是泛質數中剔除掉強質數後的泛質數，並且弱質數肯定是兩個a≥7的泛質數的積。有了泛質數、強質數和弱質數的概念後，找大質數a的問題就可通過如下三步來完成：
(1)、利用方程b=（a^2-1）/12求出所有小於a≥7的泛質數；
(2)、建立一個所有泛質數的兩兩乘積表，即弱質數表；
(3)、如果泛質數a不在弱質數表中，a就是質數，否則就是弱質數。

大質數及大合數雙質因數問題的太極分析

由於找大質數a的問題的上述三步都是P問題，所以找大質數a的問題就是P問題而不是NP問題；又由於分解雙質因數的大合數必然在弱質數表中，大合數分解雙質因數問題就可轉換成弱質數表的生成及查詢問題，弱質數表的生成問題和查詢問題都是P問題，所以大合數分解雙質因數問題也是P問題。

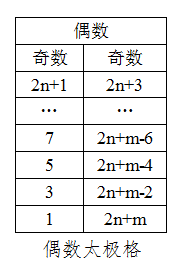
用太極格查找哥德巴赫猜想的例外偶數

陳景潤“1+2”定理講的是偶數可以表達為一個素數及一個不超過兩個素數的乘積之和，“1+（1或2）”定理

講的是偶數可以表達為強質數和強質數之和或強質數和弱質數之和。任意大偶數放入太極格觀察，針對“1+（1或2）”定理可給出如下證明：任意大偶數都是兩奇數之和，奇數之和的集合就可構成一個偶數太極格（見右圖），易知：太極格中的強質數和弱質數的個數總數大於太極格中奇數個數總數的二分之一。故，偶數必然可以表達為強質數和強質數之和或強質數和弱質數之和。繼續觀察上述偶數太極格會發現，隨著偶數的增大，由質數方程可知，太極格右列的弱質數越來越多，強質數越來越少，相鄰強質數之間的跨度會越來越大，已知質數個數是無窮多個，偶數太極格右列的質數個數則會趨於1。又由於1不是質數，偶數太極格右列僅有的一個質數+1就是例外偶數，也即出現例外偶數是必然的，“1+1”是不成立的。例外偶數的具體查找方法是：針對偶數太極格右列最下端（和1對應）2n+m(m為奇數)出現的每一個質數，編制一個簡單電腦程式來判斷這樣一種情況，當2n+m為質數時，2n+m和（2n+m+1）/2閉區間之內的所有奇數中，只有2n+m是質數，其他都是非質奇數。這時候，1不是質數，2n+m+1是偶數，該偶數就是哥德巴赫猜想的例外偶數。四色理論的太極證明

太極計算更適於證明四色理論，我們先將地圖劃分成太極格，其中每個太極格周圍用兩種顏色就可區分，再給選中的某個方格配一個顏色後，任何一個太極格用三種顏色即可。接著將某一個方格以及周圍方格拓撲變形成某一國家和周圍國家的形狀，如果這個國家周圍有偶數個國家，三種顏色足夠描述，如果是奇數個國家，再增加一種顏色即可。任何一個國家周圍不是奇數個國家就是偶數個國家，所以說任何一張地圖用四種顏色足夠描述。

太極計算的前景

將太極計算引入數學理論之後，太極計算變成了一個非常有效的數學工具，是數學計算在方法論範疇的一次標誌性進步。太極計算的標誌性成果是自然語言太極計算機（軟量子計算機），自然語言太極計算機的出現標誌著機器人又向生物人靠近了小步，這一小步會直接影響到人類生活的一大步。所以說，太極計算理論在未來資訊時代不可避免的會成為數理邏輯算的一塊新的奠基石，它是未來數理邏輯的“希望之星”或“燎原之火”，一定會在人類數學大廈中綻放出璀璨奪目的智慧光芒。