定義
多項式時間(英語:Polynomial time)在計算複雜度理論中,指的是一個問題的計算時間{\displaystyle m(n)}不大於問題大小{\displaystyle n}的多項式倍數。任何抽象機器都擁有一複雜度類,此類包括可於此機器以多項式時間求解的問題。
數學描述
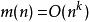 多項式時間
多項式時間以數學描述的話,則可說 ,此k為一常量值(依問題而定)。
數學家有時把“如多項式時間長的算法”視為 快速計算,相對應的是 超多項式時間,表示任何多項式時間的輸入數目只要夠大,超多項式時間所需的解題時間終究會大大超過任何多項式時間的問題。指數時間就是一例。
可以在決定型依序機器上(例如圖靈機)以多項式時間解決的決定性問題,其屬於的複雜度類被稱為P。可以在多項式時間驗證答案的決定性問題稱為NP。而NP也是可以在非確定型圖靈機以多項式時間解決的問題(NP兩字為 Non-deterministic Polynomial的縮寫)。
多項式時間在決定型機器上是最小的複雜度類,且在機器模型改變時依舊強韌,且也是可在副程式組合過程中保持封閉的類別。
強多項式時間指的是此問題的運算時間不因輸入數據的數字大小而變動,而是依照輸入數據的結構複雜度(例如圖論中的頂點數量)。
解釋
超多項式時間:O(c^f(n)),其中c為大於1的常數,f(n)大於常數,小於線性。
可以在決定型依序機器上(例如圖靈機)以多項式時間解決的決定性問題,其屬於的複雜度類被稱為P。可以在多項式時間驗證答案的非決定性問題稱為NP。而NP也是可以在非確定型圖靈機以多項式時間解決的問題(NP兩字為 Non-deterministic Polynomial的縮寫)。
多項式時間在決定型機器上是最小的複雜度類別,且在機器模型改變時依舊強韌,且也是可在副程式組合過程中保持封閉的類別。
強多項式時間指的是此問題的運算時間不因輸入資料的數字大小而變動,而是依照輸入資料的結構複雜度。
多項式時間的副類別[
•常量時間:O(1)
•線性時間:O(n)
•平方時間:O(n^2)
•立方時間:O(n^3)

