基本介紹
 NP問題
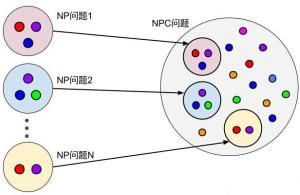
NP問題首先需要介紹P(Polynomial,多項式)問題.P問題是可以在多項式時間內被確定機(通常意義的計算機)解決的問題.NP(Non-Deterministic Polynomial, 非確定多項式)問題,是指可以在多項式時間內被非確定機(他可以猜,他總是能猜到最能滿足你需要的那種選擇,如果你讓他解決n皇后問題,他只要猜n次就能完成----每次都是那么幸運)解決的問題.這裡有一個著名的問題----千禧難題之首,是說P問題是否等於NP問題,也即是否所有在非確定機上多項式可解的問題都能在確定機上用多項式時間求解.
這樣一來,只要我們找到一個NPC問題的多項式解,所有的NP問題都可以多項式時間內劃歸成這個NPC問題,再用多項式時間解決,這樣NP就等於P了.
換一種說法,如果一個問題的複雜度是該問題的一個實例規模n的多項式函式,則這種可以在多項式時間內解決的問題屬於P類問題.通俗地稱所有複雜度為多項式時間的問題為易解的問題類,否則為難解的問題。
有些問題很難找到多項式時間的算法(或許根本不存在),例如“找出無向圖中哈密頓迴路”問題。但如果給了該問題的一個答案,可以在多項式時間內判斷這個答案是否正確。例如說對於哈密頓迴路問題,給一個任意的迴路,很容易判斷它是否是哈密頓迴路(只要看是不是所有的頂點都在迴路中就可以了)。這裡給出NP問題的另一個定義,這種可以在多項式時間內驗證一個解是否正確的問題稱為NP問題,亦稱為驗證問題類。
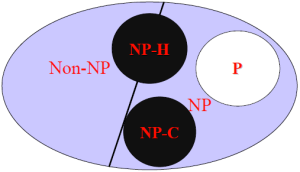
簡單的說,存在多項式時間的算法的一類問題,稱之為P類問題;而像梵塔問題,推銷員旅行問題等問題,至今沒有找到多項式時間算法解的一類問題,稱之為NP問題。同時,P類問題是NP問題的一個子集。
歷史
1971年,史蒂芬·庫克(Stephen A. Cook)發表了 The Complexity of Theorem Proving Procedures(定理證明過程的複雜性)。把以多項式時間解決為衡量標準的問題歸成三大類,即NP(nondeterministic poly-nomial),NP完全(NP-complete)與NP難度問題。
非確定性問題
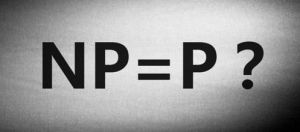 NP問題
NP問題人們發現,所有的完全多項式非確定性問題,都可以轉換為一類叫做滿足性問題的邏輯運算問題。既然這類問題的所有可能答案,都可以在多項式時間內計算,人們於是就猜想,是否這類問題,存在一個確定性算法,可以在指數時間內,直接算出或是搜尋出正確的答案呢?這就是著名的NP=P?的猜想。解決這個猜想,無非兩種可能,一種是找到一個這樣的算法,只要針對某個特定NP完全問題找到一個算法,所有這類問題都可以迎刃而解了,因為他們可以轉化為同一個問題。另外的一種可能,就是這樣的算法是不存在的。那么就要從數學理論上證明它為什麼不存在。
有些看來好像是非多項式的問題,其實是多項式問題,只是人們一時還不知道它的多項式解而已。