大系統穩定性理論
正文
基於穩定性的定義不同,分析大系統穩定性的方法有兩種:①李雅普諾夫函式法(見李雅普諾夫穩定性理論)。考慮系統輸入為零時,研究在初始狀態激勵下大系統內部狀態運動特性的穩定性,這是自動控制理論中李雅普諾夫意義下的穩定性的推廣。②輸入輸出法。考慮輸入的作用,研究大系統在零初始條件下,對系統的有界輸入是否會產生有界輸出,這是輸入輸出特性意義下的穩定性。這兩種方法雖然分析問題的角度不同,但有相同的解題思路:確認大系統穩定性既依賴於各子系統的穩定性,又和各子系統之間的關聯有關,故都採用分解技術,將大系統分解為幾個孤立子系統,並以適當形式關聯而合成大系統(見表)。先按系統穩定性理論研究各子系統的穩定性,並設法定量地測算其穩定程度,同時定量地測運算元系統之間關聯的強弱對合成大系統穩定性的影響,根據這些測算找到某種條件去判斷合成大系統的穩定性,稱為大系統穩定性判據。關於分析大系統穩定性的判據,人們已提出許多不同的型式,但都是充分條件,而沒有一個必要條件。用穩定性的充分條件判定失敗,還不能說明這個大系統是不穩定的,而只有用不穩定性的充分條件判定成功後,才能認定這個大系統是不穩定的,反之亦然。 大系統穩定性理論
大系統穩定性理論
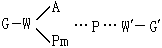
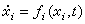 的穩定性。對於每個子系統可分別作出李雅普諾夫函式Vi(xi,t), 同時定義合成大系統的加權和李雅普諾夫函式為
的穩定性。對於每個子系統可分別作出李雅普諾夫函式Vi(xi,t), 同時定義合成大系統的加權和李雅普諾夫函式為 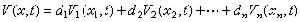
上述李雅普諾夫穩定性判據的優點是允許在合成大系統中有個別孤立子系統是不穩定的,只要略加數學上的處理,判據仍能適用;這種穩定性判句的缺點是尋找李雅普諾夫函式較困難,沒有一個確定的通用方法,通常只能參照以往的研究成果,根據大系統的具體情況反覆探求。
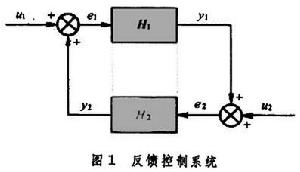
小增益定理 用來給出系統的有界輸入產生有界輸出的充分條件。它是輸入輸出法的理論基礎。圖1所示反饋控制系統中,u1、u2為系統的輸入;y1、y2為系統的輸出;e1、e2為誤差信號;H1、H2為系統本身的特性。明顯地存在以下關係:
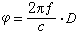
 大系統穩定性理論
大系統穩定性理論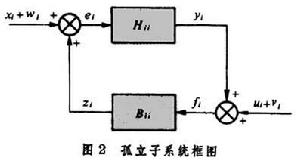 大系統穩定性理論
大系統穩定性理論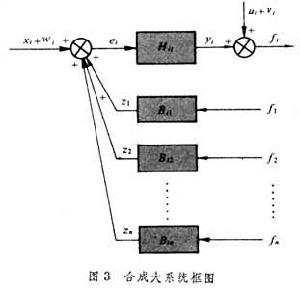 大系統穩定性理論
大系統穩定性理論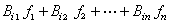 可以定量地計算各子系統之間的關聯程度。用數學方法認定以上關係都是有界的,各子系統的穩定程度的測度整體上大於各子系統的關聯強度,則整個大系統是輸入輸出穩定的。
可以定量地計算各子系統之間的關聯程度。用數學方法認定以上關係都是有界的,各子系統的穩定程度的測度整體上大於各子系統的關聯強度,則整個大系統是輸入輸出穩定的。 參考書目
A.N.Michel,R.K.Miller, Qualitative Analysis ofLarge Scale Dynamic Systems, Academic Press, NewYork,1977.

