motion，stabilityof
物體或系統在外干擾的作用下偏離其運動後返回該運動的性質。若逐漸返回原運動則稱此運動是穩定的，否則就是不穩定的。對任何運動，外干擾都是經常存在的，因此可以說，物體或系統的某一運動的穩定性就是它的存在性，只有穩定的運動才能存在。在工程技術上，要使設計對象的某些運動能夠實現，那些運動必須是穩定的。運動是一切事物的變化過程，所以研究運動的穩定性，涉及所有科學技術領域，包括社會科學。1892年俄國數學家A.M.李亞普諾夫開創了運動穩定性研究的新紀元。他提出解決運動穩定性問題的兩個方法：第一，是通過求解系統的微分方程分析運動的穩定性；第二，(直接法)是定性的方法，它不需求解微分方程，而是尋求具有某些性質的函式(稱李亞普諾夫函式)，使這些函式與微分方程相聯繫，就可控制積分軌線的動向。李亞普諾夫第二方法是目前解決運動穩定性問題的基本方法，已在套用數學、陀螺力學、自動控制、航空航天等領域廣泛套用。當今，如不作說明，運動穩定性常被理解為李亞普諾夫穩定性。
線性系統的穩定性有3種：穩定、臨界情況和不穩定，它們分別對應於李亞普諾夫意義下的漸近穩定、穩定和不穩定。線性系統有以下兩個常見的數學模型：①高階微分方程
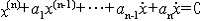，式中x(i)表示x的i階導數，ai為標量係數。②一階微分方程組
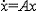，式中A為n×n常值陣。下面分別給出這兩個數學模型代表的線性系統的穩定性定理。①高階微分方程線性系統穩定性定理。若上面第一個方程的特徵根，即特徵方程λn＋a1λn-1＋…＋an-1λ＋an＝0的根，均具有負實部，則系統穩定；有一個零根或一對虛根而其餘根有負實部，則系統屬臨界情況；其他情況下，系統不穩定。為避免求根而直接由方程的係數判別系統的穩定性，有代數判據：A.赫維茨判據和E.J.勞思檢驗法。②一階方程組線性系統穩定性定理。若上面第二個方程組的特徵根，即特徵方程det【λΙ－A］＝0的根，均具有負實部，則系統穩定；有一個正實部的根，則系統不穩定；實部為零的根代數重數等於其幾何重數且其餘根均有負實部，則屬臨界情況；實部為零的重根代數重數大於幾何重數，則系統不穩定。定常非線性系統的穩定性設n維定常非線性系統的運動由向量微分方程
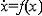描述，式中x為n維狀態向量；
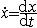，t為流逝時間。設g(t)是它的一個已知特解，即系統的一個已知運動，則有
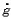(t)＝f〔g(t)〕。若系統於初始時刻t0受到初始擾動，初始狀態由g(t0)變到x0，則初始擾動為y0＝x0－g(t0)。記初始條件為(t0，x0)的受擾運動為x(t)＝x(t；t0，x0)，則運動g(t)的擾動變數為y(t)＝x(t)－g(t)。直接微分可得擾動y(t)應滿足的擾動微分方程
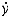(t)=F(y，t)。研究系統
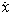=f(x)的運動g(t)的穩定性問題，等價於研究g(t)的擾動y(t)的擾動微分方程的原點y(t)＝0的穩定性問題，因為x(t)→g(t)等價於y(t)→0。李亞普諾夫穩定性定義有穩定、漸近穩定、不穩定3種類別。①設系統由向量微分方程
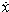=f(x)描述，g(t)是它的一個特解。若系統於初時刻t0受到初始擾動，初始狀態由g(t0)變到x0，則初始擾動為x0－g(t0)。記由初始條件(t0，x0)決定的受擾運動為x(t)＝x(t；t0，x0)。若任取正數ε和t0≥0，都可找到另一正數δ＝δ（ε，t0），對任何初擾動滿足‖x0－g(t0)‖＜δ都有‖x(t；t0，t0)－g(t)‖＜ε對一切t≥t0成立，則稱g(t)是穩定的。②若運動g(t)是穩定的，且t→∞時，‖x(t)－（t）‖→0，則稱g（t）是漸近穩定的；③若運動g(t)不滿足穩定條件，則稱它是不穩定的。李亞普諾夫穩定性定義是局部性的，只要ε、δ存在使定義成立，而不管它們多小，都稱，g(t)是穩定、漸近穩定或不穩定的。後來又建立了全局漸近穩定的定義，這時的初始擾動y。可以任意大。全局穩定性是工程技術上所要求的性質。李亞普諾夫建立了關於漸近穩定、穩定和不穩定的定理，從而奠定了穩定性理論的基礎。後來被補充了很多新定理，如關於全局穩定的定理等。李亞普諾夫穩定性定理已成為解決非線性系統穩定性的重要理論和方法並被普遍地套用，通稱李亞普諾夫方法或v函式法。但其套用強烈地依賴於（t）的構造，而這正是一個十分困難的問題。
李亞普諾夫函式用以證明穩定性所構造的滿足穩定性定理的函式，泛稱李氏函式或v函式。每一個系統都需構造自己的李氏函式，才能確定其穩定性。最簡單最常用的是二次齊次式形式的v函式。
李亞普諾夫第一近似理論利用一次近似判別非線性系統零解穩定性的理論。在原點將系統方程展開為正整冪級數：
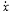=f(x)=Ax+f2(x),其
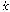=Ax是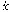
=f(x)的第一近似系統，即線性系統，f2(x)是含高次項的部分。第一近似定理指出：若A的特徵根均有負實部，則原系統漸近穩定；若A至少有一個特徵根的實部為正，則原系統不穩定；若A有實部為零的特徵根，而其他特徵根的實部非正，則原系統的穩定性由高次項f2（x）決定。因大量實際問題可用一次近似描述，所以李亞普諾夫第一近似理論在工程中廣為套用。