對穩定性的認識—從種群到生態系統
穩定性—涉及生態系統的各個層面
就如同人們在不同的時空尺度使用生態系統、生物群落和種群一樣,人們也常常在不同的時空尺度談論穩定性問題,因此就可能有諸如“長期穩定性”之類的說法,但在生態學領域,多數研究主要涉及中小時空尺度的穩定性問題。
良性生態系統穩定性的維持機制一直都是套用生態學家關注的重要問題之一,因為只有闡明了穩定性的機制,才有可能在生產或保護實踐中維持或調控目標生態系統的穩定存在或發展。關於穩定性的機制,人們特別關注多樣性或複雜性與穩定性之間的關係。
認識發展的幾個關鍵節點
20世紀50年代,以MacArthur(1955)為代表的生態學家試圖構建與種群間相互作用(如捕食者—被捕食者)為核心的生態穩定性理論,主要是在種群和群落水平。20世紀70年代初,人們對生態系統的認識(雖然也還是基於捕食者—被捕食者這樣較簡單系統的分析)從單一的平衡狀態到多個平衡狀態的轉變(Holling 1973),宣告了理論生態學家的傑作—生態可塑性概念的粉墨登場。20世紀90年代初,以Scheffer為代表的生態學家(Scheffer et al. 1990)開始以水生態系統(特別是湖泊生態系統)為例,研究生態系統在不同狀態間的轉化問題(即所謂穩態轉化),這或許因為湖泊生態系統(特別是淺水湖泊)在人類活動的干擾(如營養鹽輸入)下,在較短的時間尺度(數年至數十年),出現明顯的狀態(如濁水—清水)轉化。
種群和群落穩定性—概念與度量
何謂“種群穩定性”和“群落穩定性”?
MacArthur於1955年在Ecology的論文“動物種群的波動,及群落穩定性的度量”堪稱關於穩定性的經典之作,該文給“種群穩定性”和“群落穩定性”下了簡單而直觀的定義:種群穩定性—“在一些生物群落,物種豐度趨於十分穩定,而在另一些群落,物種豐度變化很大,將前者稱為穩定,後者稱為不穩定”;群落穩定性—“在一些生物群落,……,由於一些原因,一個物種異常增殖,如果另外種類的豐度由於前者而顯著變化,則稱群落不穩定,如果異常增殖的物種對其它物種的影響越小,群落就越穩定”。
MacArthur的群落穩定性定義雖簡單,但到底指什麼還是不甚明確,譬如“對群落中其它種的影響”可以有多種不同的解讀,它可能指平均(所有種)最大豐度變化,或者指相對變化、或者指平均平方變化,或者不同的種類能被不同的權重等。在植物群落的演替研究中,植被演替過程中某一演替階段的穩定性或許更有價值。
此外,如果從生態對策的角度來審視種群的穩定性問題,還是挺有意義的。一般來說,個體大、繁殖速度慢的K-對策物種的種群穩定性較好,而個體小、繁殖速度快的r-對策物種的種群穩定性較差。因此,K-對策物種是對所謂“穩定性環境”的一種適應,而r-對策物種是對所謂“非穩定性環境”的一種適應。這不僅在解釋短期的種群行為或許在解釋地質環境變化過程中不同生態對策物種的進化上也會具有意義。
種群和群落穩定性的概念—動聽卻難以度量
如何度量種群穩定性?依據MacArthur的定義似乎難以對種群穩定性進行嚴格的度量。也許可以考慮兩種度量辦法:1)對大小完全不同的物種,用內稟增長率r的大小或許可以判斷穩定性的大小;2)對於大小和繁殖率相近的物種,也許可以用比較種群波動的振幅、頻率的大小或者震盪的不規則性來進行度量。直觀地說,振幅越大、頻率越高、震盪越不規則,則種群越不穩定。
如何度量群落穩定性就更為困難了。人們常常將食物網的複雜程度(如能量流動途徑或食物鏈結點數)與群落穩定性直觀地聯繫起來,即直觀地(當然也是基於一定的經驗)認為能量在食物網中流動的途徑越多,群落穩定性越大(Odum 1953)。MacArthur(1955)運用綿密的邏輯分析力圖證實這一觀點的合理性。
MacArthur首先通過對種群豐度的二種極端情形的定性分析試圖說明其推論的合理性,即一種情形是一個群落中某一物種的種群異常的大,為了減少其對群落中其它種群的影響,必須有大量的捕食者去分散過剩的能量,該物種必須有大量的餌料種群不至於使種群減少太多,也就是說,通過每個物種的多種(能量流動)途徑的存在是減少一個種類的種群過剩效應所必須;另一種情形是一個群落中某一物種的種群異常的小,為了將其對群落中其它種群的影響減少到最小,該種的每一種捕食者應該有大量的可替代食物以減少對稀有種的壓力,同時也能將其自身的種群豐度維持在與原來非常接近的水平。因此,這二種情形中的任一種都表明通過食物網的可選擇能量流動途徑的多寡度量了穩定性。
接下來,MacArthur依據對生態現象的經驗性觀察,直覺地賦予了群落穩定性若干特性:1)穩定性隨食物鏈結點(link)增加而增加,直覺上似乎是如果一個物種僅有一種捕食者和一種食物(餌料),其穩定性應該最小;2)如果每個物種的餌料物種數目一定,群落中物種數的增加將增加穩定性;3)一定程度的穩定性可通過大量的物種(每種的食物相當局限)或通過少量的物種每種捕食許多其它物種來實現;4)對一個有m個物種的群落,但有m個營養級且每個物種捕食其下面的所有物種時,穩定性將達到最大,如果一個物種捕食其它所有種類且這些種類全在一個營養級時,穩定性將達到最小。因此,食譜變窄將降低穩定性,但卻是效率所必須,二者都是在自然選擇壓力下生存所需要的特性,自然選擇可能使動物在保證必要的穩定性條件下使效率達到最大化。
最後,MacArthur用上述賦予的特性,試圖解釋北極和熱帶地區的群落穩定性問題:1)在物種稀少的北極地區,很難或不可能獲得穩定的食物供給,獵食者不得不捕食廣泛的食物種類,也能期待見到許多營養級(相對於物種數而言),即便如此,也難以保證穩定性,因此在北極地區,種群容易劇烈波動;2)而在物種豐富的熱帶地區,即便是十分狹窄的食譜也能獲得所需的穩定性,物種能沿著特定的線路特化,營養級可能相對較少(相對於物種數而言)。
MacArthur的觀點雖被廣泛引用,但是無論是關於種群還是群落穩定性,都無法進行定量的度量,主要局限於為人們提供對種群和群落穩定性進行精神思辨的食糧。
系統穩定性—概念與度量
用簡單的系統詮釋複雜的系統穩定性
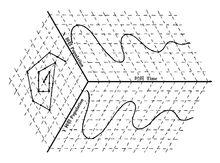 圖1 二個種群數量的時間變化導出的相平面
圖1 二個種群數量的時間變化導出的相平面Holling(1973)從純理論的角度研究了一個非常簡單的系統(只有二個種群組成)的行為。二個相互作用的種群可以是捕食者—被捕食者,或牧食動物—被牧食植物或二個競爭者。他圖示了如何用相平面來刻畫二個種群之間相互作用的軌跡。相平面概念是Poincare H 於 1885 年首先提出來的,是求解一、二階線性或非線性系統的一種圖解法,常用來分析系統的穩定性。
構想在一個恆定環境中向一個或二個種群施加的擾動將導致種群波動,其振幅將逐漸減小,這可用圖1來表示,這裡每個種群的時間波動顯示在盒子的側面。在這個例中,二個種群在某種意義上是相互調控的,但是滯後回響導致了一系列的振動,其每個種群的振幅逐漸減小到一個恆定的值。但是,如果我們也關心持續性(persistence),那我們將不僅想知道這二個種群是如何從特定的一對初始值開始其行為軌跡,而且想知道所有可能的成對值,因為也許就存在若干個初始種群組合可導致二個種群中的一個或另一個滅亡。但是,在時間軸上顯示可能回響的全部變化是非常困難的,而在相平面上繪出軌跡被證明是方便的,如圖4-1盒子底部所示,這裡的二個軸表示二個種群的密度。在平面上的軌跡表示在一定的時間間隔二個種群序列的變化,每個點表示每個種群在特定時間點的特有的密度,箭頭表明時間變化的方向。如果振動衰減,如顯示的例子,該軌跡將呈現一個封閉的螺旋,最終達到一個穩定的平衡。
接下來,Holling描述了相平面中各種不同形式的軌跡,並定義了各種各樣的數學或系統學上的穩定性概念:圖4-2A為一個開放的螺旋,表示波動的振幅逐漸增加,添加的小箭頭暗示無論何種種群組合來啟動軌跡都是這樣的結局;圖4-2B的軌跡是封閉的,任何出發點都會回到那一點,尤其重要的是每個出發點都產生一個獨特的環,這些點不傾向於匯集到一個單一的環或點去,這也稱為中性穩定性(neutral stability),這是一個理想的無摩擦的擺鐘顯示的穩定性;圖4-2C顯示的是一個與圖4-1類似的穩定系統,這裡相平面中所有可能的軌跡都螺旋進一個平衡。這三個例子都相對簡單,但與經典的穩定性分析有關,也可能正是生態學的理論好奇之處。
圖2D~2F增加了一些複雜性,在某種意義上,圖2D是A和C的組合,在相平面的中央,所有可能的軌跡都向內螺旋進平衡,而在這個區域外的都向外螺旋,最終導致的一個或另一個滅絕。這與圖2C的全域穩定性(global stability)相反,是一個局域穩定性(local stabilty)的例子。他指定表現穩定性的區域為吸引域(domain of attraction),包含該域的線為吸引域的邊界(boundary)。圖2E的行為正好相反,在一個內部的區域,軌跡向外螺旋至一個穩定極限環(a stable limit cycle),如果越過了該環,軌跡再向內接近它。最後,圖2F顯示一個穩定節(stable node),此時無震盪,軌跡單調地接近節點。這六種圖形能以幾乎無限變化方式組合產生若干吸引域,在其中能見到穩定平衡、穩定極限環、穩定節點或中性穩定軌道。
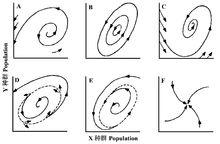 圖2 相平面中系統可能的行為案例
圖2 相平面中系統可能的行為案例Holling認為,這之前的傳統模型的行為特點是1)要么是全域穩定或者是全域不穩定,2)中性穩定性非常不可能,以及3)當模型穩定時,極限環就是一個可能的結果。圖2 顯示了相平面中系統可能的行為案例,(A)非穩定的平衡,(B)中性穩定平衡,(C)穩定平衡,(D)吸引域,(E)穩定極限環,(F)穩定節點(引自Holling 1973)
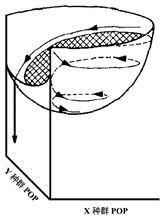 圖3 軌跡在勢場上移動的反饋力的略圖
圖3 軌跡在勢場上移動的反饋力的略圖Holling形象地可用一個缽(bowl)來表示勢能場(potential field)(圖3),如果整個勢能場為一個淺缽,系統將為全域穩定,所有軌跡將旋向缽底—平衡點;但如果至少有一個較低的(如獵物)滅絕閾值,缽的一邊將撕開一個裂口(如圖3),如果軌跡啟動位置過高的話,較大的振幅將攜帶其超越該裂口,而只有那些正好避開了裂口最低點的軌跡才能旋進缽底。可將缽稱為吸引盆(basin of attraction),那么吸引域(domain of attraction)將由周期性行為和力的構型所決定。圖3為軌跡在勢場上移動的反饋力的略圖,陰影部分表示吸引場(引自Holling 1973)。
大膽外延—從單個到多個平衡狀態的新系統觀
Holling(1973)認為傳統的系統觀僅聚焦於系統在某個平衡點附近的行為,而忽略了系統可能在多個平衡狀態間的轉換:僅關注個體死亡、種群消失和物種滅絕,譬如在一些年份貓頭鷹多、老鼠少,而在另外的年份,情況相反;又如魚類種群隨自然條件有盛有衰;再如昆蟲種群極端變化到只有對數轉換才容易表示;此外,在不同的區域,經過或長或短的時間,物種能完全消失,然後又再現。
Holling認為,傳統的系統觀更多的是直觀的和表象的,科學的系統觀不應該只關注有機體數量的多寡及它們數量的恆定程度,因為一個原始(未被擾動)的生態系統在自然歷史進化的長河中可能經歷了多個不同的平衡狀態,在人類活動(資源利用、污染等)的影響下,生態系統可能從一個平衡狀態轉變(退變)到另一個平衡,常常導致嚴重的生態後果(如物種瀕危甚至消失)。因此,科學的系統觀應聚焦於並充分認識多平衡狀態及其鄰域條件,從這種角度來審視生態系統的行為將可能獲得不同但有用的見解,而基於上述二種不同世界觀的策略可能恰好是對立的。
在這裡,筆者不得不感嘆的是理論生態學家借用相平面圖以及用僅有2個種(這比任何一個自然生態系統都簡單得不能再簡單的了)的相互作用的理論軌跡勾勒出了系統穩定性的框架,並大膽地擴展到談論生態系統的穩定性問題。簡單地說,Holling(1973)用這種巧妙的手法,試圖讓人們相信複雜的自然生態系統中也存在多穩定域(multiple stability domains)或多吸引域(multiple basins of attraction),以及它們是如何與時空尺度下的生態過程、隨機事件(如干擾)和異質性相關聯的。
系統穩定性的度量—一樣困難
與種群和群落穩定性的度量一樣,系統穩定性的度量也是一件極其困難之事。Pimm(1991)認為,一個系統若且唯若所有的變數在擾動後都返回了最初的平衡才被認為是穩定的,如果這僅適用於小干擾,則系統為局域穩定(locally stable),如果系統能從所有可能的干擾均能返回,稱為全域穩定(globally stable),系統返回特定平衡相關的變數的所有數值的集合稱為吸引域,穩定性是無量綱的(non-dimensional),二進制的,0表示不穩定,1表示穩定。
Gallopin(2006)認為,常用的穩定性概念聚焦平衡點或軌跡附近系統的行為,可通過干擾後系統返回穩定點或軌跡的速度來度量,這本質上就是Pimm(1984)定義的可塑性概念,後來被Holling(1996)稱之為工程可塑性,這也相等於在數學裡熟知的局部穩定性概念。
迄今為止,還是沒有一個大家普遍接受的系統穩定性的度量方法,還只是停留在定性的描述而已。這可能是由於上述系統穩定性概念來源於理論生態學家對非常簡單的生態系統(僅由二個物種組成)的抽象,而一個複雜的生態系統(如熱帶雨林)則可能由成千上萬個物種錯綜複雜地相互聯繫與交織在一起,二者相差甚遠,而且理論生態學家也沒有對所涉及的生態系統的時空尺度予以界定。即便如此,生態系統的多穩定狀態是現實存在的,從理論生態學角度提出的系統穩定性概念依然具有重要價值。
穩定性景觀—形象地描繪多穩態系統
一些學者還試圖通過形象的方式表示一個含有多個穩態的系統,將系統的多個穩定狀態抽象地圖示在一起,稱之為“穩定性景觀(stability landscape)”,這是一種直觀地描繪系統的動態特徵(包括各穩態之間的相互關係)的手法,這裡的景觀類似於景觀生態學中景觀的含義,但它純粹是抽象的。
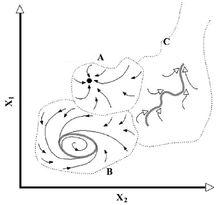 圖4 系統的“穩定性景觀”
圖4 系統的“穩定性景觀”Gallopin(2006)圖示了具有3個域的1個系統,A域含有一個穩態(steady state),B域含有一個穩定圈(stable cycle),C域含有一個穩定軌跡(stable trajectory);整個圖描繪了系統的“穩定性景觀”,由所有吸引域的構型所表征,包括區分它們的邊界;穩定性景觀格局是系統結構的一部分,依賴於系統的參數賦值(固定的或非常緩慢變化的因素)(圖4)。圖4顯示 擁有2個變數(X1、X2)3個吸引子(A、B、C)的狀態空間,虛線表示各自的吸引域(引自Gallopin 2006)。
在一個擁有多個吸引子的動態系統,一些關鍵參數的連續變化能導致系統穩定性景觀的不連續變化(圖5),這些不連續體(discontinuities)在動態系統數學理論中稱為分叉(bifurcations),在災害理論中稱為災變(catastrophes)。
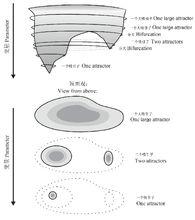 圖5 吸引子的定性變化
圖5 吸引子的定性變化需要指出的是,穩定性景觀依然是一種描述性的概念模式,還無法定量化,因此也只是一種理論生態學家對系統穩定性的形象思考。圖5表示吸引子的定性變化。1個參數的連續變化能引起吸引子萎縮、分裂或消失。上圖是三維的表示,下圖是頂面觀,立體圖形的3個剖面(引自Gallopin 2006)
穩態轉化
生態系統發育具有階段性,即具有相對穩定的暫態,這些暫態之間的變化稱之為穩態轉化。穩態轉化也是一種從量變到質變的生態系統突變過程。穩態轉化以生態系統狀態對環境條件的回響軌跡為基礎:生態系統狀態在一定範圍內回響相當遲緩,而接近某一臨界水平時強烈地回響,形成突變;當生態系統的回響曲線向回“摺疊”時表明,在同樣的環境條件下,生態系統可存在於兩種不同的穩定狀態之中,被一個不穩定的平衡區隔開。
穩態轉化理論在湖泊生態系統的管理中具有重要的套用價值。多穩態理論認為,富營養化對淡水生態系統的結構、功能和穩定性有著明顯的負面影響,但是,人們仍然不清楚在一個突變點出現之前富營養化是如何通過化學計量效應使生態系統去穩定化的。
最近的研究發現 ,高內穩性植物占優勢的生態系統傾向於具有更穩定的狀態,而低內穩性植物占優勢的生態系統更為機會主義,對外界的擾動更為脆弱,即:富營養化通過首先抑制高內穩性的沉水植物群落來使湖泊生態系統去穩定化,但低內穩性的沉水植物群落由於較低的突變閾值而先行崩潰,這恰好可用作湖泊生態系統從清水到濁水轉化的早期預警信號。但同時由於低內穩性植物具有較快的恢復能力,因此可作為生態修復的先鋒物種(圖6)。化學計量內穩性在決定沉水植物占優勢的湖泊生態系統的結構、穩定性和可塑性中扮演的角色具有重要意義。
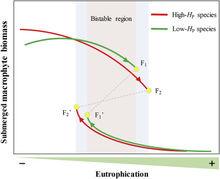 圖6解釋淺水湖泊穩態轉化機制與過程的模式圖
圖6解釋淺水湖泊穩態轉化機制與過程的模式圖