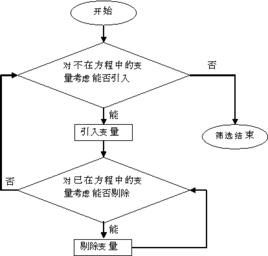
定義
在處理測量數據時,經常要研究變數與變數之間的關係。變數之間的關係一般分為兩種。一種是完全確定關係,即函式關係;一種是相關關係,即變數之間既存在著密切聯繫,但又不能由一個或多個變數的值求出另一個變數的值。例如,學生對於高等數學、機率與統計、普通物理的學習,會對統計物理的學習產生影響,它們雖然存在著密切的關係,但很難從前幾門功課的學習成績來精確地求出統計物理的學習成績。但是,對於彼此聯繫比較緊密的變數,人們總希望建立一定的公式,以便變數之間互相推測。回歸分析的任務就是用數學表達式來描述相關變數之間的關係。
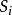 多元回歸
多元回歸1、多元回歸是指一個因變數(預報對象),多個自變數(預報因子)的回歸模型。基本方法是根據各變數值算出交叉乘積和 。
2、這種包括兩個或兩個以上自變數的回歸稱為多元回歸。套用此法,可以加深對定性分析結論的認識,並得出各種要素間的數量依存關係,從而進一步揭示出各要素間內在的規律。一般來說,多元回歸過程能同時提供多個備選的函式關係式,並提供每個關係式對實驗數據的理解能力,研究者可以結合自己的理論預期,據此作出選擇。
數學模型
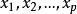 多元回歸
多元回歸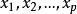 多元回歸
多元回歸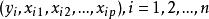 多元回歸
多元回歸相關變數之間的關係可以是線性的,也可以是非線性的。這裡只討論多元線性回歸。設 是p個可以精確測量或可控制的變數。如果變數y與 之間的內在聯繫是線性的,那么進行n次試驗,則可得n組數據:
它們之間的關係可表示為:
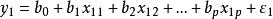 多元回歸
多元回歸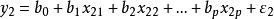 多元回歸
多元回歸………………
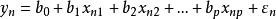 多元回歸
多元回歸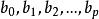 多元回歸
多元回歸其中, 是p+l個待估參數,εi表示第i次試驗中的隨機因素對yi的影響。為簡便起見,將此n個方程表示成矩陣形式:
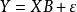 多元回歸
多元回歸其中
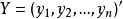 多元回歸
多元回歸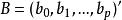 多元回歸
多元回歸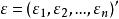 多元回歸
多元回歸上式便是p元線性回歸的數學模型。
最小估乘
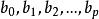 多元回歸
多元回歸為了求出多元線性回歸模型中的參數 ,可採用最小二乘法,即在其數學模型所屬的函式類中找一個近似的函式,使得這個近似函式在已知的對應數據上儘可能和真實函式接近。
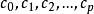 多元回歸
多元回歸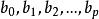 多元回歸
多元回歸設 分別是 的最小二乘估計,則多元回歸方程(即近似函式)為:
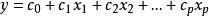 多元回歸
多元回歸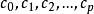 多元回歸
多元回歸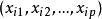 多元回歸
多元回歸 多元回歸
多元回歸 多元回歸
多元回歸 多元回歸
多元回歸 多元回歸
多元回歸其中 叫做回歸方程的回歸係數。對每一組,由回歸方程可以確定一個回歸值。這個回歸值與實際觀測值之差,反映了與回歸直線
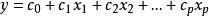 多元回歸
多元回歸 多元回歸
多元回歸 多元回歸
多元回歸 多元回歸
多元回歸 多元回歸
多元回歸的偏離程度。若對所有的觀測數據, 與 (I=1,2,…,n)的偏離越小,則認為回歸直線與所有試驗點擬合得越好。全部觀測值 與回歸值 的偏差平方和為:
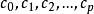 多元回歸
多元回歸根據微分學中的極值原理 應是下列方程組的解:
通過整理可將上述方程組寫成如下形式:
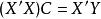 多元回歸
多元回歸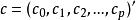 多元回歸
多元回歸其中, ,稱為回歸方程的係數矩陣,X'是X的轉置矩陣。當X'X滿秩時,逆矩陣(X'X)-1存在,係數矩陣C可以表示為:
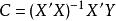 多元回歸
多元回歸上式即為回歸模型中參數B的最小二乘估計。至此,我們就得到了p元線性回歸方程。
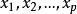 多元回歸
多元回歸建立回歸方程的目的是要利用它來進行預報與控制。在實際問題中,事先並不能斷定隨機變數y與 之間確有線性關係,在求解回歸方程前,線性回歸模型只是一種假設,所以在求出線性回歸方程之後,還需對其進行統計檢驗,給以肯定或否定的結論。有關回歸方程及回歸係數的顯著性檢驗問題,這裡就不介紹了。
線性處理
由於線性回歸方程比較簡單,所以在遇到非線性模型時,最好將其轉換為線性模型。
(1)多項式模型
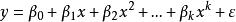 多元回歸
多元回歸多項式模型為 ,
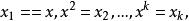 多元回歸
多元回歸對方程中的變數作如下變換
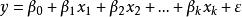 多元回歸
多元回歸則原方程變為,
就可用線性模型的方法處理。
(2)指數模型指數模型為:
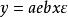 多元回歸
多元回歸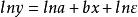 多元回歸
多元回歸方程兩邊取對數得:
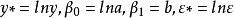 多元回歸
多元回歸令
則可得線性方程
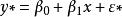 多元回歸
多元回歸(3)冪函式模型冪函式模型為:
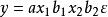 多元回歸
多元回歸方程兩邊取對數得
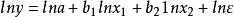 多元回歸
多元回歸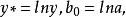 多元回歸
多元回歸令
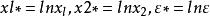 多元回歸
多元回歸則冪函式模型就變為線性模型
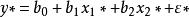 多元回歸
多元回歸(4)成長曲線模型
成長曲線模型在經濟、教育和心理研究中都非常有用,其數學表達式為:
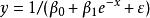 多元回歸
多元回歸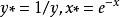 多元回歸
多元回歸令 ,
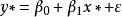 多元回歸
多元回歸它就轉化為線性模型:
套用
(1) 確定幾個特定的變數之間是否存在相關關係,如果存在的話,找出它們之間合適的數學表達式;
(2) 根據一個或幾個變數的值, 預測或控制另一個變數的取值,並且可以知道這種預測或控制能達到什麼樣的精確度;
(3) 進行因素分析。例如在對於共同影響一個變數的許多變數(因素)之間,找出哪些是重要因素,哪些是次要因素,這些因素之間又有什麼關係等等。