外角和

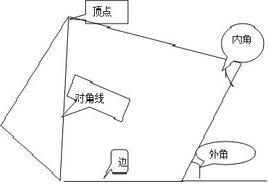
多邊形都會有內角,與之對應的是外角,即將其中一條邊延長後,延長線與另一條邊成的夾角,稱為外角。多邊形外角的總和叫做外角和。任意多邊形的外角和都為360°，與邊數無關。

計算公式

通常內角+外角=180度，所以每個外角中分別取一個 相加，得到的和成為多邊形的外角和。n邊形的內角與外角的總和為n×180°，n邊形的內角和為（n-2）×180°，那么n邊形的外角和為360°。這就是說多邊形的外角和和邊數無關。解答有關多邊形內角和外角和的問題時，通常利用公式列方程來解答問題。並且，三角形的一個外角等於不相鄰的兩個內角之和。