多邊形的外角和

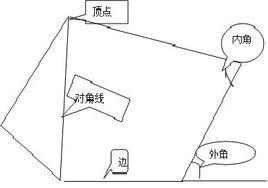
與多邊形的內角相對應的是外角，多邊形的外角就是將其中一條邊延長並與另一條邊相夾的那個角。任意凸多邊形的外角和都為360°。多邊形所有外角的和叫做多邊形的外角和。 證明：根據多邊形的內角和公式求外角和為360 n邊形內角之和為(n-2)*180,設n邊形的內角為∠1、∠2、∠3、...、∠n,對應的外角度數為：180-∠1、180°-∠2、180°-∠3、...、180°-∠n，外角之和為： (180-∠1)+(180°-∠2)+(180°-∠3)+...+(180°-∠n) =n*180°-(∠1+∠2+∠3+...+∠n) =n*180°-(n-2)*180° =360° MJ20161104

證明

∵n邊形外角等於（180-和他相鄰的內角）.
∴180n-180（n-2）=180n-180n+360=360
180n是所有外角和內角的和,180（n-2）是所有內角和,減去就是外角和.
由上式可知任意多邊形的外角和等於360度