基本介紹
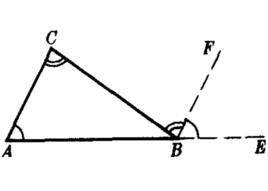
三角形外角定理三角形的任意一個外角等於和它不相鄰的兩個內角之和。如圖，△ABC的一個外角∠CBE=∠A+∠C。
這個定理的證明，如圖所示，利用平行線的性質證明；也可以直接用三角形內角和定理證。
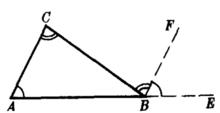圖1 由三角形外角定理不難推出：三角形任意一個外角，大於和它不相鄰的任意一個內角。如圖，∠CBE>∠A，∠CBE>∠C 。
三角形外角定理的證明
證法一
利用三角形內角和定理證明有
∠1=∠A，∠2=∠B，∴ ∠1+∠2=∠A∠B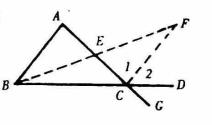(圖2) .
圖2 證法二
全等形證法
如圖2,設E為AC的中點，連BE且延長到F，使EF= BE，連CF。
在△ABE和△CEF中，
∵∠AEB=∠CEF，BE= EF，AE= EC
∴ △ABE≌△CEF
∴∠1=∠A
∴CF// AB
∴∠2=∠ABC，
∴∠1 +∠2=∠A+∠ABC，
即 ∠ACD=∠A+∠B.
推論及證明
推論 三角形的一個外角大於任何一個和它不相鄰的內角。
證法一
根據三角形內角和定理推出三角形外角定理
有∠ACD=∠A+∠B，則
∠ACD>∠A(全量大於它的任一部分)
∠ACD>∠B .
證法二
全等形證
如上面圖2，設E為AC的中點，連線BE且延長到F，使EF= BE，連CF，
在△AEB和△CEF中，
∠AEB=∠CEF，BE= EF，AE= EC，
∴△AEB≌△CEF，
∴∠ECF=∠A，
但∠ACD>∠ECF，
∴∠ACD>∠A.
其次，延長AC到G，得到∠ACD=∠BCG，作BC上的中線，並且把它延長，使延長的部分等於原來中線的長。同理可證∠BCG>∠ABC，由此可知∠ACD>∠ABC 。
證法三
反證法
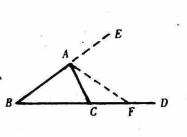圖3 
三角形外角定理 假設∠ACD ∠CAB，那么∠ACD=∠CAB，或∠ACD
