簡介
【詞語】:外擺線
【注音】:wài bǎi xiàn
【釋義】:外擺線,英文名:epicycloid,又稱圓外旋輪線。
定義
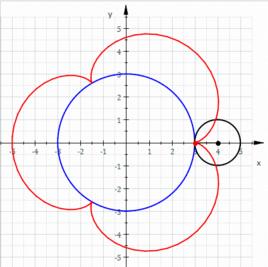
當半徑為b的“動圓”沿著半徑為a的“定圓”的外側無滑動地滾動時,動圓圓周上的一定點p所描繪的點的軌跡,就叫做外擺線。
方程
在以定圓中心為原點的直角坐標系中,其方程為
x=(a+b)cosθ-bcos[(a+b)θ/b];
y=(a+b)sinθ-bsin[(a+b)θ/b];
性質
當a/b是有理數時,它是閉曲線;
當a=b時,它就是心臟線。
早在公元前140年前後,希臘天文學家希帕克就知道此種曲線。
德沙格在1639年,歐拉在1781年分別圓外旋輪線,德沙格首次用此種曲線來設計齒輪的齒形。
圓內旋輪線(內擺線)
定義
當半徑為b的圓沿著半徑為a(a>b)的圓的內側無滑動滾動時,動圓圓周上一點p的軌跡。
方程
在以定圓中心為原點的直角坐標系中,其方程為
X=(a-b)cosθ+bcos[(a-b)θ/b];
Y=(a-b)sinθ-bsin[(a-b)θ/b];
心臟線
心臟線是外擺線的一種,其n為 2,亦可以極坐標的形式表示: r =a( 1 - sin θ)。方程為ρ(θ) = a(1 + cosθ)的心臟線的面積為:S=3(πa^2)/2。
在直角坐標系中方程:(x^2+y^2-ax)^2=a^2(x^2+y^2)(x^2表示x的平方)