介紹
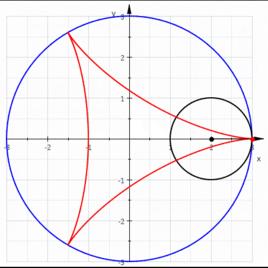
內擺線，指的是一個動圓內切於一個定圓作無滑動的滾動，動圓圓周上一個定點的軌跡。它與擺線相當，但是它不是線上上做純滾動的圓，而是在大圓內表面做純滾動的圓。
參數方程
內擺線如果較小圓具有半徑r，而較大圓具有半徑 ，則曲線的參數方程可以由下式給出：
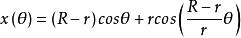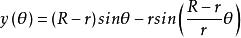內擺線
內擺線或者
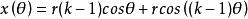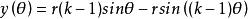內擺線
內擺線（1）如果k是整數，那么曲線是閉合的，並且曲線有k個尖峰（即尖角，曲線不可微分）。特別地，對於k = 2，曲線是直線，圓圈稱為卡爾達諾圓。卡爾達諾圓是第一個描述內擺線及其在高速印刷中的套用。
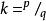內擺線（2）如果k是一個有理數，用最簡單的術語表示 ，則曲線具有p個尖點。
（3）如果k是非理性數，則曲線永遠不會閉合，並且填充較大圓和半徑為R-2r的圓之間的空間。
舉例
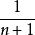內擺線假設有一個定圓，若有另一個半徑是剛才的圓形的 倍的圓在其內部滾動，則圓周上的一定點在滾動時劃出的軌跡是一條內擺線（圓內螺線）。
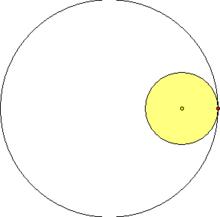內擺線三尖瓣線（Deltoid，字自「Delta」Δ）是內擺線（圓內螺線）一種，其n為2（或1/2）。
星形線 （Astroid）是內擺線（圓內螺線）一種，其n為 3。
內擺線是一種特殊類型的長短輻圓。
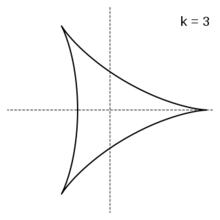k=3，三尖瓣線
k=4，星形線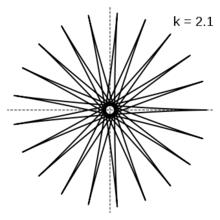
k=2.1
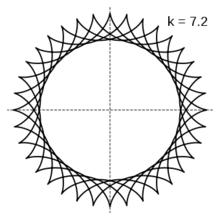k=7.2與群的關係
任何具有整數值為k的內擺線（因此具有k個尖點），能夠在另一個具有k+1個尖點的內擺線裡面移動，使得較小的下擺線的點總是與較大的相連線。 這個運動看起來有點像“滾動”，雖然它不是在經典力學的意義上滾動，因為它涉及滑動的概念。
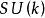內擺線
內擺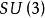線
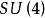內擺線內擺線的形狀可以與表示為 的特殊單位組相關聯，其由具有行列式1的k×k個單位矩陣組成。例如， 中的矩陣的對角項的和的允許值是正好位於內擺線的三個尖點的複雜平面內的點。 同樣地，矩陣的對角項相加的和依此類推。
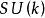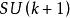內擺線
內擺線由於這個結果，可以使用作為一個子群在內移動的事實來證明具有k個尖點的外擺線也可以在具有k+1個尖點的內擺線內移動。
衍生曲線
在中心有極點的內擺線是玫瑰曲線。
內擺線
和內擺線相似的曲線可以用萬花尺來繪製。 具體來說，萬花尺可以畫出內擺線和外擺線。
基於Steelmark的匹茲堡鋼人員的標誌包括具有四個尖點的內擺線。 在“周二早晨四分衛”的每周NFL.com專欄中，格雷戈·伊斯特布魯克（Gregg Easterbrook）經常將鋼人隊稱為“內擺線”。 智利足球隊瓦奇巴托體育俱樂部根據鋼人隊的標誌，並以內擺線為特色
