埃爾米特插值多項式逼近
正文
埃爾米特插值是一種常見的插值方法。假設在區間【α,b】上給定了n個互不相同的點x1,x2,…,xn以及一張數表 (*)
(*)
 ,
,
 為結點組的埃爾米特插值多項式。如果定義在【α,b】上的函式 ƒ(x)在xk(k=1,2,…,n)處有αk-1階導數,並取
為結點組的埃爾米特插值多項式。如果定義在【α,b】上的函式 ƒ(x)在xk(k=1,2,…,n)處有αk-1階導數,並取 ,則稱相應的Hn(x)為ƒ(x)的以
,則稱相應的Hn(x)為ƒ(x)的以 為結點組的(α1,α2,…,αn)階埃爾米特插值多項式。作為特殊情況,若諸αk都為1,則Hn(x)就是ƒ(x)的拉格朗日插值多項式;若n=1,則Hn(x)為ƒ(x)的α1-1階泰勒多項式。最使人們注意的是諸αk都為2的情況,這時Hn(x)為次數不高於2n-1的代數多項式。如果寫
為結點組的(α1,α2,…,αn)階埃爾米特插值多項式。作為特殊情況,若諸αk都為1,則Hn(x)就是ƒ(x)的拉格朗日插值多項式;若n=1,則Hn(x)為ƒ(x)的α1-1階泰勒多項式。最使人們注意的是諸αk都為2的情況,這時Hn(x)為次數不高於2n-1的代數多項式。如果寫 


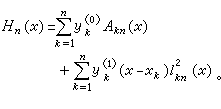
 ,而給
,而給 以適當的限制。這個想法大致起源於拉格朗日插值多項式的研究。為了改善插值多項式的逼近度,需對其導數作一定的要求。
以適當的限制。這個想法大致起源於拉格朗日插值多項式的研究。為了改善插值多項式的逼近度,需對其導數作一定的要求。 為了簡單,考慮定義區間為【-1,1】的情況。L.費耶爾首先讓
 ,稱
,稱 



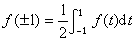 。
。
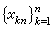 是取在開區間(-1,1)中的,而2n+1次代數多項式Q2n+1(ƒ,x)滿足條件
是取在開區間(-1,1)中的,而2n+1次代數多項式Q2n+1(ƒ,x)滿足條件 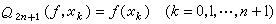 ,
,
 。
。
 為Xn(x)的零點全體,則
為Xn(x)的零點全體,則  。
。
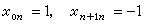 ,
,
 ,
,
 為結點組的埃爾米特-費耶爾插值多項式序列Fn+2(ƒ,x),對於 ƒ(x)=x2這樣好的函式,也會在(-1,1)中處處發散。而取
為結點組的埃爾米特-費耶爾插值多項式序列Fn+2(ƒ,x),對於 ƒ(x)=x2這樣好的函式,也會在(-1,1)中處處發散。而取 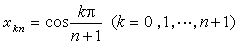
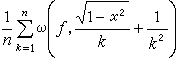 。
。
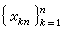 以及數組
以及數組 ,
, ,要確定一個次數不高於2n-1的代數多項式
,要確定一個次數不高於2n-1的代數多項式 使得
使得 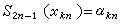 ,
,
 ,(k=1,2,…,n)。當取αkn=ƒ(γkn)時,考慮S2n-1(ƒ,x)對ƒ(x)的逼近,也可以考慮埃爾米特插值多項式對函式及其導數的同時逼近。例如,取
,(k=1,2,…,n)。當取αkn=ƒ(γkn)時,考慮S2n-1(ƒ,x)對ƒ(x)的逼近,也可以考慮埃爾米特插值多項式對函式及其導數的同時逼近。例如,取 


至於ƒ(x)的(α1,α2,…,αn)階埃爾米特插值多項式Hn(x)對ƒ(x)的逼近,如果ƒ(x)在【α,b】上有m階導數,則在【α,b】中有與x有關的點ξ使得
 ,
,
 。
。
