簡介
函式構造論包括正逆兩方面的定理。
所謂正定理就是從函式的結構性質(連續性、李普希茨條件、可微性等)來導出用n次多項式(或其他函式系)逼近函式時,其最佳逼近值(又稱最佳逼近度)趨向於零的速度估計;
所謂逆定理就是用n次多項式(或其他函式系)逼近函式時,從其最佳逼近值趨向於零的速度估計式來導出函式本身的結構性質。因此,研究函式的結構性質就可以化歸為研究用多項式(或其他函式系)逼近時,其最佳逼近值趨向於零的速度。
許多情況下,正定理和逆定理是一對互逆的命題。
函式逼近論
[approximtion theory of functions]
研究如何用某些計算簡單的函式(稱為逼近函式)近似地表示一般函式(稱為被過近函式) 的數學分支。通常逼近函式與被逼近函式屬於某個線性賦范空間.對於有限區間[a,b] 上的函式.通常採用代數多項式和樣條函式作過近函式,而對於周期函式,則採用三角多項式和樣條函式來過近。
函式過近論的研究內容除可過近性、最佳逼近理論等屬於一般逼近論範疇的問題外還有下列與函式有關的問題:
(1) 函式構造論。
(2) 線性運算元逼近(approximation by liuear operators)。最佳逼近元雖然有最好的逼近度,但它是非線性的且計算複雜套用不方便。於是,人們構造了各種有較好逼近度的線性運算元。對於周期函式,傑克遜運算元
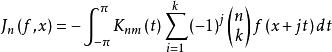 函式構造論
函式構造論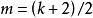 函式構造論
函式構造論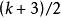 函式構造論
函式構造論是比較理想的逼近工具,其中,若 k 為偶數;,若 k 為奇數;且
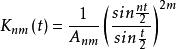 函式構造論
函式構造論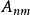 函式構造論
函式構造論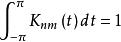 函式構造論
函式構造論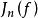 函式構造論
函式構造論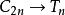 函式構造論
函式構造論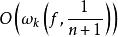 函式構造論
函式構造論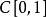 函式構造論
函式構造論係數 是使的規範常數。運算元 是(n 階三角多項式的全體的集)但線性運算元,其逼近誤差可用 來估計。對於 中的函式,最經典的運算元為伯恩斯坦多項式運算元
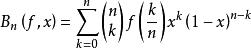 函式構造論
函式構造論這是一個線性正運算元。
 函式構造論
函式構造論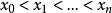 函式構造論
函式構造論 函式構造論
函式構造論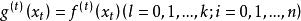 函式構造論
函式構造論(3)插值逼近 (approximation by interpolation) 。設 f 是 上(連續或 k 次連續可微)但函式, 是上 n+1 個點,稱為 插值節點,簡稱節點。插值逼近是指滿足插值條件的逼近函式 g 來逼近 f 。通常,採用代數多項式、三角多項式、樣條函式作為逼近函式。
 函式構造論
函式構造論 函式構造論
函式構造論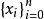 函式構造論
函式構造論拉格朗插值多項式 (Lagrange interpolation polynonial) 是最簡單的插值逼近工具。設 是上的連續函式, 是插值節點,n 次代數多項式
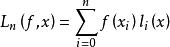 函式構造論
函式構造論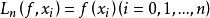 函式構造論
函式構造論是滿足的唯一確定的 n 次代數多項式,稱為 n 次拉格朗日插值多項式,其中
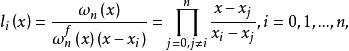 函式構造論
函式構造論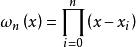 函式構造論
函式構造論假如除了滿足函式值的插值條件外還滿足各類導數或高階導數的插值條件就得到埃爾米特插值多項式。對周期函式可仿照代數多項式構造拉格朗日三角插值多項式。
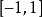 函式構造論
函式構造論 函式構造論
函式構造論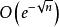 函式構造論
函式構造論(4) 有理函式逼近(approximation by rational functions)。有理函式是兩個代數多項式之比,其中分母在所考慮的自變數區間內不等於零。在切比雪夫研究多項式逼近的同時也就已經考慮了有理函式的最佳逼近理論。但真正受到重視是在1964 年紐曼(D.J.Newman) 發現用 n 次有理麗數在上通近麗數的過近度可以達到的驚人結果發表以後。許多與代數多項式逼近問題可對有理函式通近作平行的討論。例如,關於有理逼近的正定理和逆定理也都已建立。
(5) 極值問題(extremum problem)。函式逼近論中出現大量的極值問題。除單個函式的最佳逼近外,人們還常常考慮計算最佳逼近在某個函式類中的上確界,計算線性運算元逼近偏差關於函式類的主項。此外,還有寬度問題等。這些極值問題的解決有助於發現好的逼近工具。
(6) 複變函數逼近(approximation by function of complex variable)。研究用特殊的解析函式近似地表示複變函數的複分析的分支。逼近的可能性,逼近速度以及各種表示方法的研究構成了復變麗數巡近論的基本內容。常用的逼近工具有插值序列、正交多項式。法貝爾多項式、連分式、冪級數和指數多項式序列,狄利克雷級數等。許多問題可以與實變函式情況平行地提出。例如,藉助多項式逼近和有理逼近中最佳逼近元的存在性唯一性以及特徵刻畫等。還有各種極值問題和偏差估計都是人們感興趣的問題。

