源來
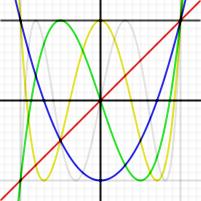 切比雪夫多項式
切比雪夫多項式切比雪夫多項式在逼近理論中有重要的套用。這是因為第一類切比雪夫多項式的根(被稱為切比雪夫節點)可以用於多項式插值。相應的插值多項式能最大限度地降低龍格現象,並且提供多項式在連續函式的最佳一致逼近。
基本性質
對每個非負整數n, Tn(x) 和 Un(x) 都為 n次多項式。 並且當n為偶(奇)數時,它們是關於x 的偶(奇)函式, 在寫成關於x的多項式時只有偶(奇)次項 。
 切比雪夫多項式
切比雪夫多項式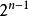 切比雪夫多項式
切比雪夫多項式n 1時,Tn的最高次項係數為 ,n=0時係數為1。
切比雪夫多項式分類
在微分方程的研究中,數學家提出切比雪夫微分方程:
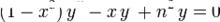 切比雪夫多項式
切比雪夫多項式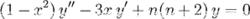 切比雪夫多項式
切比雪夫多項式相應地,第一類和第二類切比雪夫多項式分別為這兩個方程的解 。
第一類切比雪夫多項式
由以下遞推關係確定
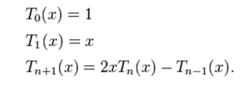 切比雪夫多項式
切比雪夫多項式也可以用母函式表示
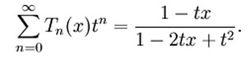 切比雪夫多項式
切比雪夫多項式第二類切比雪夫多項式
由以下遞推關係給出
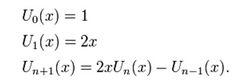 切比雪夫多項式
切比雪夫多項式此時母函式為
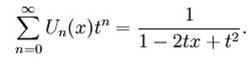 切比雪夫多項式
切比雪夫多項式兩類切比雪夫多項式間的關係
兩類切比雪夫多項式間還有如下關係 :
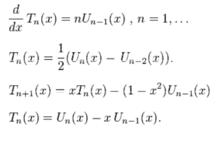 切比雪夫多項式
切比雪夫多項式切比雪夫多項式是超球多項式或蓋根堡多項式的特例,後者是雅可比多項式的特例。
切比雪夫多項式導數形式的遞推關係可以由下面的關係式推出:
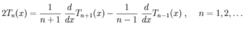 切比雪夫多項式
切比雪夫多項式套用
切比雪夫多項式在逼近理論中有重要的套用。這是因為第一類切比雪夫多項式的根(被稱為切比雪夫節點)可以用於多項式插值。相應的插值多項式能最大限度地降低龍格現象,並且提供多項式在連續函式的最佳一致逼近。
切比雪夫多項式插值
切比雪夫多項式在逼近理論中有重要的套用。這是因為第一類切比雪夫多項式的根(被稱為切比雪夫節點)可以用於多項式插值 。相應的插值多項式能最大限度地降低龍格現象,並且提供多項式在連續函式的最佳一致逼近。
冪級數項數的節約
設f(x)在(1,1)上的近似展開式為
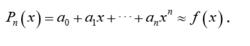 切比雪夫多項式
切比雪夫多項式若
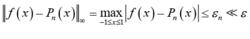 切比雪夫多項式
切比雪夫多項式 切比雪夫多項式
切比雪夫多項式其中 是給定的誤差限.可以利用切比雪夫多項式將Pn(x)重新組合以降低逼近多項式的次數。記
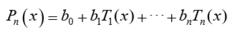 切比雪夫多項式
切比雪夫多項式若
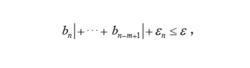 切比雪夫多項式
切比雪夫多項式而
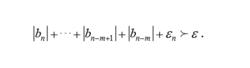 切比雪夫多項式
切比雪夫多項式則可以把後面m項去掉,得到f(x)新的,n-m次的並滿足誤差要求的逼近多項式
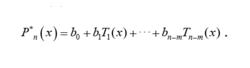 切比雪夫多項式
切比雪夫多項式事實上,只要注意
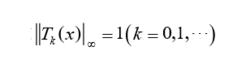 切比雪夫多項式
切比雪夫多項式並利用範數的三角不等式,容易證明
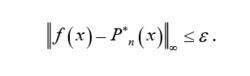 切比雪夫多項式
切比雪夫多項式切比雪夫多項式一直是研究熱點,目前已發現了許多良好的性質,如正交性、奇偶性、有界性、完備性等,產生了不少恆等式,得到了一些積和式,對第一類切比雪夫多項式構成的遞推關係式、不動點、方程(組)也有了初步的研究成果,對切比雪夫型基本方程組全體複數解的一般表示及其周期軌表示、二維切比雪夫型方程組也出現了更深入的研究。有的學者則研究了其在分子軌道方面的套用,在Fibonacci數的套用,還有學者研究了與切比雪夫多項式相關的行列式。