簡介
 埃爾米特插值
埃爾米特插值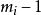 埃爾米特插值
埃爾米特插值 埃爾米特插值
埃爾米特插值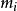 埃爾米特插值
埃爾米特插值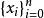 埃爾米特插值
埃爾米特插值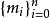 埃爾米特插值
埃爾米特插值埃爾米特插值是另一類插值問題,這類插值在給定的節點處,不但要求插值多項式的函式值與原函式值相同。同時還要求在節點處,插值多項式的一階直至指定階的導數值,也與被插函式的相應階導數值相等,這樣的插值稱為 埃爾米特(Hermite)插值。 Hermite插值在不同的節點,提出的差值條件個數可以不同,若在某節點,要求插值函式多項式的函式值,一階導數值,直至 階導數值均與被插函式的函式值相同及相應的導數值相等。我們稱 為 重插值點節,因此,Hermite插值應給出兩組數,一組為插值點 節點,另一組為相應的重數標號 。
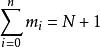 埃爾米特插值
埃爾米特插值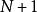 埃爾米特插值
埃爾米特插值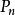 埃爾米特插值
埃爾米特插值若 ,這就說明了給出的插值條件有 個,為了保證插值多項式的存在唯一性,這時的Hermite插值多項式應在 上求得,於是可作如下定義。
定義
 埃爾米特插值
埃爾米特插值 埃爾米特插值
埃爾米特插值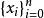 埃爾米特插值
埃爾米特插值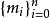 埃爾米特插值
埃爾米特插值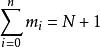 埃爾米特插值
埃爾米特插值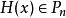 埃爾米特插值
埃爾米特插值設 為 上充分光滑函式,對給定的插值定節 ,及相應的重數標號 , 時,若有 滿足
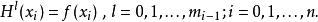 埃爾米特插值
埃爾米特插值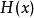 埃爾米特插值
埃爾米特插值 埃爾米特插值
埃爾米特插值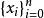 埃爾米特插值
埃爾米特插值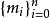 埃爾米特插值
埃爾米特插值則稱 為 關於節點 及重數標號 的Hermite插值多項式 。
二重Hermite插值多項式
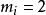 埃爾米特插值
埃爾米特插值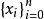 埃爾米特插值
埃爾米特插值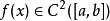 埃爾米特插值
埃爾米特插值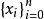 埃爾米特插值
埃爾米特插值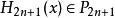 埃爾米特插值
埃爾米特插值常用的埃爾米特插值為 的情況,即給定的插值節點 均為二重節點,更具體些, ,及插值節點 ,若有 滿足
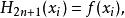 埃爾米特插值
埃爾米特插值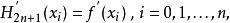 埃爾米特插值
埃爾米特插值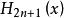 埃爾米特插值
埃爾米特插值 埃爾米特插值
埃爾米特插值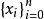 埃爾米特插值
埃爾米特插值就稱 為 關於節點 的二重Hermite插值多項式 。
相關定理
1.唯一性定理
 埃爾米特插值
埃爾米特插值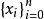 埃爾米特插值
埃爾米特插值關於節點 的二重Hermite插值多項式存在且唯一。
2.誤差定理
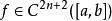 埃爾米特插值
埃爾米特插值 埃爾米特插值
埃爾米特插值 埃爾米特插值
埃爾米特插值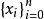 埃爾米特插值
埃爾米特插值若,則為關於上節點的二重Hermite插值多項式誤差為
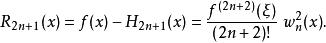 埃爾米特插值
埃爾米特插值這裡,
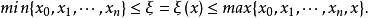 埃爾米特插值
埃爾米特插值