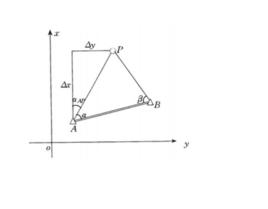
測量方法
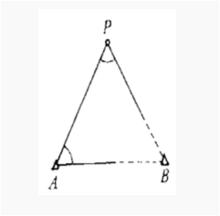側方交會A,B兩點坐標已知，A(Xa，Ya)，B(Xb,Yb)。通過觀測∠A和∠P，測定未知點P的平面坐標，這種方法稱為側方交會。
全站儀架設在A點，測量∠PAB，全站儀架設在P點，測量∠APB。
已知A,B坐標，可以計算出距離AB和AB方位角Fap。
∠PBA=180°-∠PAB-∠APB，AP/sin∠PBA=AB/sin∠APB，
所以可以計算出距離AP
P點坐標Xp=Ax+AP×cos(Fab-∠PAB)
P點坐標Yp=Ya+AB×sin(Fab-∠PAB)
側方交會的精度分析
在中國中鐵五局一公司日常測量工作中，常採用經緯儀交會法加密控制點(簡稱圖根點)。根據已知控制點的條件和地形情況，經緯儀交會法分前方交會，側方交會和後方交會三種。石灰石礦的測量人員多用側方交會，因為側方交會可在待定點直接擺站，進行驗收等測量，從而節約時間減少工作量。本文擬對側方交會的精度進行分析，並尋找規律。
一般規範規定：(1)選(圖根控制)點時，所求點必須和三個以上的已知控制點通視。交會角γ不小於30°，不大於150°，即要求最不利的圖形的點位中誤差，不大於交會角γ=90°時點位中誤差的兩倍(容許誤差)。(2)選點時，要求點的位置要選在土質堅實、埋設標誌後不易損壞和不會變動的地方。本文就與規範的第一條規定有關係的側方交會精度進行分析。
側方交會法及精度
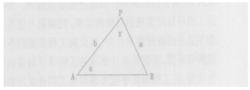（1）側方交會
側方交會如圖A、B為兩已知點，在已知點A和未知點P上設站，觀測角α和交會角γ，以決定P點位置的方法，叫側方交會。側方交會求未知點的坐標和前方交會求未知點的坐標套用相同的公式。因此，推導側方交會點位精度公式思路和推導前方交會點位精度公式的思路是一致的。即先求AP邊邊長b及方位角α的真誤差公式，而後求未知點P的坐標真誤差公式，再轉化成中誤差公式，最後導出P點點位中誤差的公式(這裡暫時假定已知點的精度較高，它們對低一級網影響較小可略而不計)。
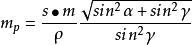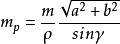側方交會
側方交會或
（2）側方交會的精度
由式看出，除了測角精度對m有影響外，而且布網圖形也對m有影響。當a+s為定值，γ=90°時，m為極小值，即布設交會角γ=90°的圖形最為理想，但是在作業中，布設γ=90°的側方交會圖形通常是困難的，所以和前方交會一樣，允許γ角在一定範圍內變動，即要求γ角不小於30°或不大於150°，使得最大誤差(容許誤差)不大於交會角γ=90°時點位中誤差的兩倍。那么，要求最不利圖形的點位中誤差不大於交會角γ=90°時點位中誤差的兩倍，是否γ角就是不小於30°或不大於150°呢?也就是說，γ角究竟在什麼樣的範圍內?我們將對側方交會的精度進行具體分析。
（3）側方交會精度的具體分析
表1 不同圖形結構點位中誤差情況表以交會角γ每15°的間隔變化試求m的變化狀況。 交會角γ以15°的間隔變化及與測角α、β相對大小變化(也以15°為間隔)，組成45種圖形結構，由求m的公式分別求得m～m(見表1)。
由表1可知當交會角γ=90°時，組成的五種圖形，其點位中誤差m～m互不相等，而且m到m也不集中形成最小值局域。因此，說交會角γ=90°的圖形最理想是不嚴謹的，不確切的。要求最不利圖形的點位中誤差不大於γ=90°時點位中誤差的兩倍，則要確定γ=90°時點位中誤差的標準，我們只好選取γ=90°時點位中誤差為最小的m，計算分析其它44種圖形，其點位中誤差與γ=90°時點位中誤差m的相對關係。
（4）側方交會時交會角 γ=30°的圖形點位中誤差精度分析
側方交會時，交會角γ=30°的圖形結構共有9種，它們的點位中誤差與γ=90°時m的相對關係見表1。
由表1可知：
①側方交會交會角γ=30°的9種圖形結構，它們的點位中誤差均不小於γ=90°時m的兩倍，最大的達到4.329倍，顯然，要遵守一般規範，保證側方交會最不利圖形的點位中誤差不大於交會角γ=90°時點位中誤差的兩倍，則交會角γ不能等於30°。
②側方交會交會角γ=30°的9種圖形結構中m=m，m=m，m=m，也就是說，儘管圖形有變化，測角α不同，但按點位中誤差的結果來看，實質上只有六種圖形結構。
③交會角γ=30°不變，測角α<90°時，隨著測角α的增大，點位中誤差增大，當測角α=90°時點位中誤差最大。α>90°後，隨測角α的增大，點位中誤差減小。
（5）側方交會時交會角 γ=45°的圖形點位中誤差精度分析
側方交會時，交會角γ=45°的圖形結構共有8種，它們的點位中誤差與γ=90°時m的相對關係見表1。由表可知：
①側方交會交會角γ=45°的8種圖形結構中，只有測角α小於等於45°的三種圖形結構的點位中誤差(m、m、m)，才能不大於交會角γ=90°時m的兩倍，其它五種圖形點位中誤差均不符合一般規定的要求。
②側方交會交會角γ=45°的8種圖形結構中m=mm=m也就是說儘管圖形有變化，測角α不同，但按點位中誤差的結果來看，實質上只有6種圖形結構。
③交會角γ=45°不變，當測角α<90°時，隨著測角α的增大，點位中誤差增大，當測角α=90°時，點位中誤差最大，當測角α>90°後，隨著測角α的增大，點位中誤差減小。
研究結論
（1）側方交會法當交會角γ=90°時，點位中誤差不是一個確定的值，測角α愈小，點位中誤差愈小。因此，在選用側方交會時，即使交會角γ=90°，也要注意圖形結構，才能減小點位中誤差，提高測量精度。
（2）一般規範應當修改，建議：選點時，所求點必須和三個以上的已知控制點通視，要求最不利圖形的點位中誤差不大於交會角γ=90°時點位中誤差的兩倍，即交會角γ不小於60°，不大於等於150°。
（3）當交會角γ確定時，測角α<90°，隨著測角α的增大，點位中誤差增大，測角α=90°時，點位中誤差最大，測角α>90°後，隨著測角α的增大，點位中誤差減小，因此，側方交會交會角不小於60°，不大於等於150°時，還要注意測角α的選取不要選取90°。最好選取小於45°。
距離側方交會在建築施工測量中的套用
在建築工程施工測量過程中，如何快速、準確地測算出測站點的平面坐標，是測量工程師關注的一個技術問題。採用距離側方交會方法測量控制點坐標，有明確、可靠的精度，方法靈便，測量誤差易於控制，在各種規模的露天施工場地都可以廣泛運用。
交會點圖形
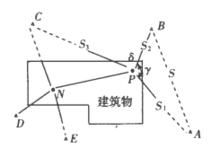圖1 交會點示意如圖1所示，A、B、C、D、E等，是分布於施工建築物周圍的工程控制點。其中，B、D點位適於架置測距反光稜鏡，稱為置鏡點。為了在建築物某一施工層面放線，可選定P點，使用全站儀觀測A、B、C三點水平方向值和測定PB(S)平距邊長。如此，我們便可利用△ABP和△BPC求得P點的平面坐標。同樣，可在另一位置測定N點。如果P、N兩點通視並且觀測，便可構成理想的交會圖形。
如在實際作業中，因受施工障礙的影響，選定的P點並不適合放線作業。這種情況下，可將P點視為己知控制點，再發展一次，形成多個放線測站點。這種“一站一點”(設一個測點，求得一個點位坐標)的交會方法稱為距離側方交會。
檢驗方法
（1）用2個交會三角形檢驗。如上所述，在P點上至少觀測3個已知點方向值，組成2個三角形，算出2組坐標進行比較。
（2）如果只能觀測到2個已知點，則必須測定2條交會邊的邊長和交會角。這樣，就有了多餘觀測量，不僅起到檢驗作用，也產生了平差問題。
（3）發展同類型控制點檢驗。如圖1發展N點，在P點和N點上相互觀測，這是最佳檢驗方法。
（4）用後方交會方法檢驗。在待定點P和N上，測3個已知方向，構成簡單的後交點圖形，可算出待定點的坐標比較。當然，後交點的定位精度與其所處圖形的位置有一定關係。待定點位於3個已知點構成的三角形內，解算成果可靠；最佳點位在已知三角形的質心附近。就所設定的作業條件而言，待定點都可處於或接近於後交圖形的最佳位置。檢核作業中所布設的測站點基本上都處於理想位置，最後成果普遍接近距離交會計算結果，坐標分量較差絕對值在2～6 mm。由此可見，後交點計算結果也可起到檢驗作用。
實際運用
（1）測設骨架控制點。在布設場區控制網的同時，採用嚴格的作業方法測定若干個可以長期利用的骨架控制點。骨架控制點分布於建築物周圍。選定的目標如避雷針、屋頂塔尖和特別設定的置鏡點標誌等。置鏡點高度應適合全站儀測距，可選在地面、樓頂、陽台等穩固部位。可採用精密方向交會和配合近距離極坐標方法，使骨架控制點的相對點位精度達到或者接近場區控制點精度。即在保持點位誤差作業指標的條件下，擴大骨架控制點的圖形。應當指出，骨架控制點的測量精度是距離側方交會方法成功的根本條件。交會圖形縮小，誤差也必然會隨之減少，這正是提高交會點精度的重要條件。
（2）使用2級全站儀。全站儀及其配件必須處於正常工作狀態。200 m以內單程測距誤差(含各種因素產生的測距誤差)應小於3 mm。須知，減小測距誤差是提高點位精度最有效的技術手段。
（3）交會角觀測方法。①交會角的測量誤差m應與測距相對誤差m/S相匹配，即m=mρ/S。採用全站儀的實際測距精度(經驗值)，求得m值，進而確定交會角觀測測回數。②作業時間充足，提倡按照規範要求進行水平方向觀測。但是，在作業條件緊迫的情況下，應當關注交會角的實際測量精度，不必計較記錄成果的形式。
（4）計算結果處理方法。如有多餘觀測量，會有幾組計算成果。就作業實驗資料看，坐標分量互差大都在1～4 mm，最大值為7 mm。最後成果選取方法：①圖形條件接近者，取平均值；②圖形條件有明顯差異，結果差值稍大，可考慮綜合條件配權，取權中數，或舍劣取優；③如果後交點計算結果的比較差值不大於4 mm，也可參與取平均值。
比較與驗證
與其他形式的測量定點方法比較，可以看出距離側方交會方法的特徵：①重要的邊、角未知量直接測量，有利於控制誤差，點位精度取決於技術努力程度；②一般情況下，都有較好的交會圖形，即交會角接近直角，容易保持邊交會的點位精度；③少設測站，減少操作誤差積累，可實現“測站對中零誤差”作業；④實際作業中，待定點雖然起自於骨架控制點，但是，待定點間相對點位誤差絕對值(可理解為相鄰點間距離誤差)，不是在起算點誤差的基數上增加，而是隨著交會圖形面積的縮小而明顯減小。為初步認識這種誤差傳播過程中的“負增長”現象，我們進行了實測驗證，誤差“負增長”現象的數學解釋就是倍乘誤差中的K值小於1。這是各種交會點圖形由大化小，誤差也隨之縮小的結果。
研究結論
（1）距離側方交會法定點精度高，且具有明顯的“誤差縮小”特徵。可通過建立適當規模的精密控制網，使交會圖形由大化小，提高放線控制點(測站點)相對點位精度，達到精確放線的目的。該法可在建築工程，如高層建築(含高塔建築)、橋樑建築，甚至某些精密安裝工程中使用。
（2）長久以來，測量工程師只重視控制“誤差放大”；應當利用“誤差縮小”特徵提高測量精度，提出新的工程測量方法。
