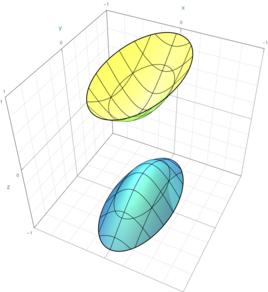
質量殼
該術語來自質量殼,也就是質量雙曲面,它表示表述如下方程的解的能量-動量空間中的雙曲面。
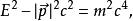 在殼
在殼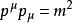 在殼
在殼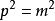 在殼
在殼這描述了靜質量為m的粒子的能量E和動量p的組合在經典狹義相對論中所允許的取值範圍;這裡的c是指光速。質量殼方程經常用四維動量來表達,並使用愛因斯坦求和約定和c= 1的單位制,也就是或者。
費曼圖中和內部傳播子相關的虛擬粒子通常允許離殼,但該進程的幅度通常隨著遠離殼而減小;傳播子通常在質量殼上有奇異點。
關於離殼集的常見誤解是它們違反能量守恆,但是實際上它們不違反能量守恆-因為能量不能在任意小的時間段內精確定義(參看測不準原理)。能量定義在越長的時間段內,它可以定義得越精確。因此,虛擬粒子的能量是測不準原理所允許的任意值(粒子的能量乘上它們存在的時間小於普朗克常數)。
(在討論傳播子的時候,滿足方程的E的負值被視為在殼的,雖然經典理論不允許粒子的能量為負值。這是因為傳播子將在一個方向承載能量和它的反粒子在另一個方向承載能量的情況總和到一個表達式中;負和正的在殼E不過就是表達了正能量的不同方向的流動。)
諾特定理
概述
諾特定理是理論物理的中心結果之一,它表達了連續對稱性和守恆定律的一一對應。例如,物理定律不隨著時間而改變,這表示它們有關於時間的某種對稱性。如果我們想像一下,譬如重力的強度每天都有所改變,我們就會違反能量守恆定律,因為我們可以在重力弱的那天把重物舉起,然後在重力強的時候放下來,這樣就得到了比我們開始輸入的能量更多的能量。
諾特定理對於所有基於作用量原理的物理定律是成立的。它得名於20世紀初的數學家埃米·諾特。諾特定理和量子力學深刻相關,因為它僅用經典力學的原理就可以認出和海森堡測不準原理相關的物理量(譬如位置和動量)。
套用
諾特定理的套用幫助物理學家在物理的任何一般理論中通過分析各種使得所涉及的定律的形式保持不變的變換而獲得深刻的洞察力。例如:
•對於物理系統對於空間平移的不變性(換言之,物理定律不隨著空間中的位置而變化)給出了動量的守恆律;
•對於轉動的不變性給出了角動量的守恆律;
•對於時間平移的不變性給出了著名的能量守恆定律。
在量子場論中,和諾特定理相似,沃德-高橋恆等式(Ward-Takahashi)產生出更多的守恆定律,例如從電勢和向量勢的規範不變性得出電荷的守恆。
諾特荷也被用於計算靜態黑洞的熵。
參看
•荷 (物理)
•拉普拉斯-龍格-冷次向量