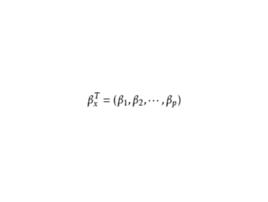回歸係數
對於回歸係數的解釋,需要從線性回歸模型當中來定義。
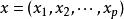 回歸係數
回歸係數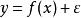 回歸係數
回歸係數線性回歸模型是一種特殊的線性模型。若變數y與變數的關係表示為,且
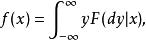 回歸係數
回歸係數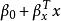 回歸係數
回歸係數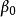 回歸係數
回歸係數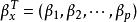 回歸係數
回歸係數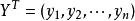 回歸係數
回歸係數稱f(x)為y對x的回歸,f(x)稱為回歸函式。通常在常態分配情形,若f(x)是x的線性函式,此時稱為線性回歸,稱為回歸常數,稱為回歸係數(regression coefficient)。取y為n個觀測,得觀測值向量,表示為如下模型:
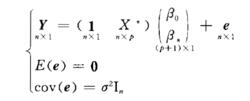 回歸係數
回歸係數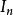 回歸係數
回歸係數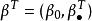 回歸係數
回歸係數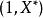 回歸係數
回歸係數其中 1是坐標全為1的向量,為n階單位陣,記,且假定這個矩陣的秩為p+1,而記
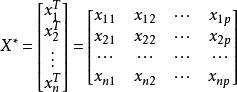 回歸係數
回歸係數這裡β,σ 為未知參數,e(n×1)是隨機向量。
最小二乘估計
回歸係數的最小二乘估計(least square estimator of regression coefficient)簡稱LS估計。參數估計的一種方法。線性回歸模型中,未知參數β的最小二乘估計為滿足
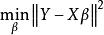 回歸係數
回歸係數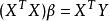 回歸係數
回歸係數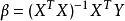 回歸係數
回歸係數的β。可知β是方程的解。此方程稱為正規方程。由於線性回歸模型中,X矩陣列滿秩,故β可解除,記為。
顯著性檢驗
回歸係數顯著性檢驗(significant test of regression coefficient)是檢驗某些回歸係數是否為零的假設檢驗。考慮線性回歸模型
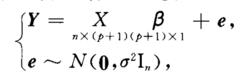 回歸係數
回歸係數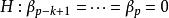 回歸係數
回歸係數不失一般性,可假定要檢驗後k個(1≤k≤p)回歸係數是否為零,即。一般用F統計量
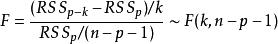 回歸係數
回歸係數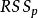 回歸係數
回歸係數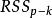 回歸係數
回歸係數去檢驗,這裡是上述模型的殘差平方和,為假定後k個係數為零時(即少了k個自變數)的模型的殘差平方和。用F檢驗有許多優良性,在這方面,中國統計學家許寶騄早期做了許多工作,後來美籍羅馬尼亞數學家瓦爾德(Wald,A.)發展了他的工作。
理解
1、相關係數與回歸係數:
A 回歸係數大於零則相關係數大於零
B 回歸係數小於零則相關係數小於零
(它們的取值符號相同)
2、回歸係數:由回歸方程求導數得到,
所以,回歸係數>0,回歸方程曲線單調遞增;
回歸係數<0,回歸方程曲線單調遞減;
回歸係數=0,回歸方程求最值(最大值、最小值)。