簡介
設D為平面區域,如果D中任一閉曲線所圍成的部分都屬於D,則稱D為平面單連通區域。直觀的說,平面單連通域就是沒有空洞的域,否則稱為復連通域。
區域
[domain]
 單連通域
單連通域 單連通域
單連通域 單連通域
單連通域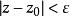 單連通域
單連通域 單連通域
單連通域 單連通域
單連通域連通的開集稱為區域。具體解釋如下:設 是複平面上的點。以為圓心,正數為半徑的開圓盤(即滿足 的一切點)稱為點的鄰域或鄰域(neighborhood)。
設 E 是複平面上的點集。如果對點 z,存在某個領域,使得這個鄰域中的點都包含在 E 中,則稱點 z 是點集 E 的一個內點(inner point)。如果 E 的每個點都是它的內點,則稱 E 是一個開集(open set)
若對於複平面上的點集 E 內任何兩點,都可用一條落在 E 內的折線將它們連線起來,則稱集合 E 為弧連通的(arcconnected)。
若複平面上的一個集合 D 既是一個開集又是弧連通的,則稱為區域。
若爾當區域
 單連通域
單連通域 單連通域
單連通域 單連通域
單連通域 單連通域
單連通域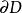 單連通域
單連通域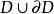 單連通域
單連通域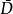 單連通域
單連通域設 D 是一個區域。如果對點,有一個鄰域使其全部不屬於 D ,則稱為區域 D 的外點(exterior point)。如果對點,在它的任意一個鄰域中,總有 D 中的點和不屬於 D 的點,則稱為 D 的邊界點(boundary point)。區域 D 的所有邊界點構成的集合,稱為區域的邊界(boundary),記作 。區域 D 連同它的邊界所組成的集合,即,稱為閉區域(closed domain),記作 。
 單連通域
單連通域如果一個區域 D 的邊界由有限個互不相交的若爾當閉曲線組成,則稱為若爾當區域(Jordan domain)。
如果一個區域 D 中任意一條若爾當閉曲線,在該區域中經過連續變形後總可以縮成該區域中的一點,則稱該區域為單連通區域(simply connected domain)。例如,整個複平面;一個圓的內部;一條帶狀的區域或者由一條若爾當閉曲線作邊界的若爾當區域,都是單連通區域。
非單連通的區域稱為多連通區域(multiply connected domain)。例如,一個環形的區域;邊界曲線多於一條的若爾當區域,都是多連通區域。
若爾當證明了下述定理:任意一條若爾當閉曲線將複平面分成兩個開區域,它們以此曲線為其公共邊界。兩個區域中有一個是有界的,稱為若爾當曲線的內部;另一個區域是無界的,稱為若爾當曲線的外部。

