定義介紹
 弧連通集
弧連通集 弧連通集
弧連通集 弧連通集
弧連通集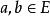 弧連通集
弧連通集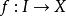 弧連通集
弧連通集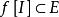 弧連通集
弧連通集設為拓撲空間的一個子集,如果對於中的任何兩點,都有一條含在E中而由a到b的道路(即),則稱E為一個 弧連通集(arcwise connectedset)。
 弧連通集
弧連通集中的極大的弧連通集稱為一個 弧連通的分支(arcwiseconnected component),X中所有的弧連通分支構成X的一個分割 。
相關定理
弧連通與連通之間有以下關係:
定理1弧連通集是連通的。
上述定理的逆命題是不成立的,如下面例題所示。
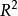 弧連通集
弧連通集例1考察平面上的子集:
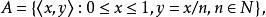 弧連通集
弧連通集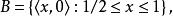 弧連通集
弧連通集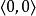 弧連通集
弧連通集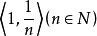 弧連通集
弧連通集 弧連通集
弧連通集 弧連通集
弧連通集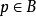 弧連通集
弧連通集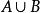 弧連通集
弧連通集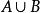 弧連通集
弧連通集其中A是由所有連結原點與點的線段上的點所組成;B是由軸上與1之間的一切點所組成。現在A與B都是弧連通的,因而也是連通的;另外,A與B又是不互相分離的,因為每點都是A的一個極限點。於是是連通的。但卻不是弧連通的,因為實際上不存在A上任何一點到B上任何一點的道路。
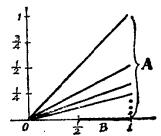 圖1
圖1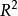 弧連通集
弧連通集平面上的拓撲學是單變數複函數論的一個重要部分。在複函數論中,把平面上的開連通集稱為一個區域(region),下面的定理在複函數論中是重要的。
 弧連通集
弧連通集定理2平面上的開連通集是弧連通的 。
弧連通空間
若拓撲空間上任意兩點可由其上的弧連線(即此弧分別以這兩點為起點和終點),則稱此空間為弧連通的,若空間有一由弧連通集組成的基,則稱為 局部弧連通空間。
 弧連通集
弧連通集 弧連通集
弧連通集局部弧連通空間是弧連通的若且唯若是連通的。
 弧連通集
弧連通集是局部弧連通的 。

