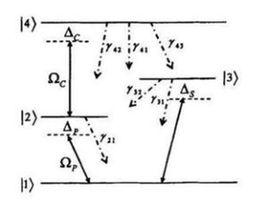
簡介
在量子力學中,在大多數情況下,哈密頓量是對應於系統的總能量的運算符。 它通常由H表示,也稱為Ȟ或Ĥ。 其頻譜是衡量系統總能量時可能產生的結果。 由於它與系統的時間演化密切相關,所以在量子理論的大多數形式中是至關重要的。
哈密爾頓人以威廉·羅文·漢密爾頓(William Rowan Hamilton)命名,他也創造了牛頓力學的革命性改革,現在稱為哈米爾頓力學,這在量子物理學中是重要的。
哈密頓量是所有粒子的動能的總和加上與系統相關的粒子的勢能。 對於不同的情況或數量的粒子,哈密頓量是不同的,因為它包括粒子的動能之和以及對應於這種情況的勢能函式。
薛丁格哈密爾頓
一個粒子
通過與經典力學類似,哈密頓量通常表示為對應於系統的動能和勢能的運算符的總和。
H=T+V(其中T是動能,V是勢能)。
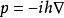 哈密頓量
哈密頓量是動量運算元,其中∇是del運算符。 ∇自身的點積是拉普拉斯運算元∇ 。
雖然這不是經典力學中哈密頓量的技術定義,但它是最常見的形式。 將這些組合在一起產生在Schrödinger方程中使用的熟悉形式:
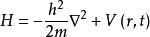 哈密頓量
哈密頓量這允許將哈密頓量套用於由波函式Ψ(r,t)描述的系統。 這是採用Schrödinger波浪力學形式學的量子力學介紹性處理方法。
人們還可以對某些變數進行替換以適應特定情況,例如涉及電磁場的一些變數。
許多粒子
由於勢能取決於顆粒的空間排列,動能也將取決於空間配置以節省能量。 由於任何一個粒子的運動將由於系統中所有其它粒子的運動而變化。 為此,動能的交點可能出現在哈密爾頓運算元中; 混合兩個顆粒的梯度:
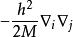 哈密頓量
哈密頓量其中M表示導致該額外動能的顆粒的集合的質量。 這種形式的術語稱為質量極化項,並且出現在許多電子原子的哈密爾頓(見下文)。
對於N相互作用的粒子,即相互作用並構成多體情況的粒子,勢能函式V不僅僅是分開的電位(並且當然不是產品,因為它在尺寸上不正確)的總和。 勢能函式只能如上所述:每個粒子的所有空間位置的函式。
對於不相互作用的顆粒,即不相互作用並獨立移動的顆粒,系統的電位是每個顆粒的單獨勢能的總和,即
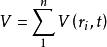 哈密頓量
哈密頓量在這種情況下,哈密頓量的一般形式是:
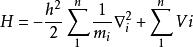 哈密頓量
哈密頓量其中所有顆粒的總和及其相應的電位;結果是系統的哈密爾頓運算元是每個粒子的單獨哈密爾頓運算元的總和。 這是一個理想的情況 - 在實踐中,粒子通常總是受到一些潛在的影響,並且有許多身體的相互作用。 這種形式不適用的兩體互動的一個說明性實例是由於帶電粒子引起的靜電勢,因為它們通過庫侖相互作用(靜電力)彼此相互作用,如下所示。
哈密爾頓方程
經典哈密頓力學中漢密爾頓方程在量子力學中有直接的類比。 假設我們有一組基本狀態n,這不一定是本能狀態的能量。為了簡單起見,我們假設它們是離散的,並且它們是正交的,我們將假設哈密爾頓運算元也是獨立於時間的。
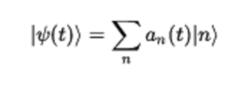 哈密頓量
哈密頓量係數a(t)是複數變數。 我們可以將它們視為指定系統狀態的坐標,例如指定經典系統的位置和動量坐標。 像古典坐標一樣,它們通常不是時間常數,它們的時間依賴性導致整個系統的時間依賴性。
這個狀態的哈密頓量的期望值也是平均能量
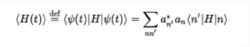 哈密頓量
哈密頓量每個an(t)實際上對應於兩個獨立的自由度,因為變數具有實部和虛部。 我們現在執行以下技巧:不使用實部和虛部作為獨立變數,我們使用(t)及其復共軛a *(t)。 通過這種自變數的選擇,我們可以計算偏導數,那么上面的方程就變成了
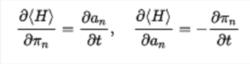 哈密頓量
哈密頓量這正是哈密頓方程的形式。
其他信息
===================================================================================
所謂哈密頓量的對角化就是解一個本徵值問題(線上性代數中就是特徵值和特徵向量)。對角化哈密頓量的過程就是一個找能量本徵值的過程(找到這個系統可能存在的能量)。或者是一個去耦合的過程(比如說兩個彈簧振子振動時存在耦合,可以寫成一個哈密頓量的形式,對角化後,找到了彈簧振子的簡振模,就去耦合了)
對角化的物理含義就是找到一個能量系統中的可能能量(一般來說這些能量都是分立的,這就是量子力學的精髓之一)
在勢場V(x)中的粒子,其經典哈密頓量H=T+V的算符表示成 Hamilton算符=動能算符+勢能,勢能是與位置X相關的量,沒有相應的算符表示,而動能算符表示為 (動量算符的平方/兩倍的質量)。 動量算符的表達形式在計算自由粒子動量平均值的過程中通過自由粒子在坐標和動量表象下的波函式變換求出。具體的公式推導可以去看量子力學。
薛丁格方程的表達形式就是哈密頓量本徵函式的形式。