簡介
哈密頓—雅可比方程(HJE)是經典哈密頓量一個正則變換,經過該變換得到的結果是一個一階非線性偏微分方程,方程之解描述了系統的行為。與哈密頓運動方程的不同之處在於 HJE 是一個偏微分方程,每個變數對應於一個坐標,而哈密頓方程是一個一階線性方程組,每兩個方程對應於一個坐標。HJE 可以漂亮地解析一些重要問題,例如克卜勒問題。
HJE 是唯一能夠將粒子運動表達為波動的一種力學表述。因此,HJE 滿足了一個長久以來理論物理的研究目標(早至 18 世紀,約翰·伯努利和他的學生皮埃爾·莫佩爾蒂的年代);那就是,尋找波傳播與粒子運動的相似之處。力學系統的波動方程與薛丁格方程很相似;但並不相同。稍後會有詳細說明。HJE 被認為是從經典力學進入量子力學最近的門階。
數學表述
哈密頓-雅可比方程是一個一階非線性偏微分方程。用數學表達
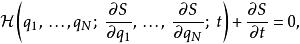 哈密頓-雅可比方程
哈密頓-雅可比方程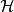 哈密頓-雅可比方程
哈密頓-雅可比方程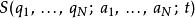 哈密頓-雅可比方程
哈密頓-雅可比方程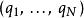 哈密頓-雅可比方程
哈密頓-雅可比方程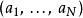 哈密頓-雅可比方程
哈密頓-雅可比方程其中, 是哈密頓量,未知函式 稱為 哈密頓主函式, 是廣義坐標, 是積分常數, t是時間 。
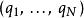 哈密頓-雅可比方程
哈密頓-雅可比方程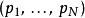 哈密頓-雅可比方程
哈密頓-雅可比方程假若能夠找到哈密頓主函式 S的形式,就可以計算出廣義坐標 與廣義動量 隨時間的演變。這樣,可以完全地解析物理系統隨時間的演化。
說明:矢量與標量分別用 粗體與 斜體顯示。例如,位置矢量通常用 r表示;而其大小則用 r來表示。
各種力學表述的比較
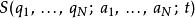 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程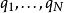 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程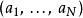 哈密頓-雅可比方程
哈密頓-雅可比方程哈密頓-雅可比方程是一個一階非線性偏微分方程;其中,函式 有 個廣義坐標 ,和 個獨立的積分常數 。在 HJE 中,哈密頓主函式 S有一個很有意思的屬性,它是一種經典作用量。
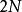 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程與拉格朗日力學的拉格朗日方程比較,哈密頓力學裡使用共軛動量而非廣義速度。並且,哈密頓方程乃是一組 個一階微分方程,用來表示 個廣義坐標和 個廣義動量隨時間的演變,而拉格朗日方程則是一組 個二階微分方程,用來表示 個廣義坐標隨時間的演變。
因為 HJE 等價於一個最小積分問題(像哈密頓原理), HJE 可以用於許多關於變分法的問題。更推廣地,在數學與物理的其它分支,像動力系統、辛幾何、量子混沌理論,都可以用 HJE 來解析問題。例如,HJE 可以用來找尋黎曼流形的測地線,這是黎曼幾何一個很重要的變分法問題。
詳解
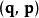 哈密頓-雅可比方程
哈密頓-雅可比方程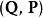 哈密頓-雅可比方程
哈密頓-雅可比方程在哈密頓力學裡,正則變換將一組正則坐標 變換為一組新的正則坐標 ,而同時維持哈密頓方程的型式(稱為 型式不變性)。舊的哈密頓方程為
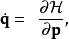 哈密頓-雅可比方程
哈密頓-雅可比方程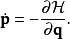 哈密頓-雅可比方程
哈密頓-雅可比方程新的哈密頓方程為
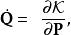 哈密頓-雅可比方程
哈密頓-雅可比方程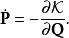 哈密頓-雅可比方程
哈密頓-雅可比方程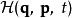 哈密頓-雅可比方程
哈密頓-雅可比方程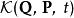 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程這裡, 、 分別為舊的哈密頓量與新的哈密頓量, 是時間。
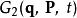 哈密頓-雅可比方程
哈密頓-雅可比方程假若,使用第二型生成函式 來生成新正則坐標,則新舊正則坐標的關係為
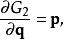 哈密頓-雅可比方程
哈密頓-雅可比方程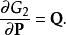 哈密頓-雅可比方程
哈密頓-雅可比方程而新舊哈密頓量的關係為
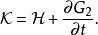 哈密頓-雅可比方程
哈密頓-雅可比方程1.哈密頓主函式
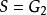 哈密頓-雅可比方程
哈密頓-雅可比方程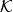 哈密頓-雅可比方程
哈密頓-雅可比方程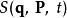 哈密頓-雅可比方程
哈密頓-雅可比方程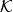 哈密頓-雅可比方程
哈密頓-雅可比方程假若,可以找到一個第二型生成函式 。這生成函式使新哈密頓量 恆等於 0 。稱這個生成函式 為 哈密頓主函式。那么,新哈密頓量 所有的偏導數都等於 0 。哈密頓方程也變得非常的簡單:
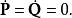 哈密頓-雅可比方程
哈密頓-雅可比方程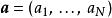 哈密頓-雅可比方程
哈密頓-雅可比方程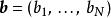 哈密頓-雅可比方程
哈密頓-雅可比方程這樣,新正則坐標都成為運動常數 、 :
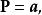 哈密頓-雅可比方程
哈密頓-雅可比方程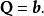 哈密頓-雅可比方程
哈密頓-雅可比方程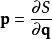 哈密頓-雅可比方程
哈密頓-雅可比方程由於 ,代入舊哈密頓量,則可得到哈密頓-雅可比方程:
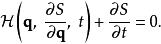 哈密頓-雅可比方程
哈密頓-雅可比方程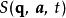 哈密頓-雅可比方程
哈密頓-雅可比方程解析問題的重要關鍵是必須找到哈密頓主函式 的方程。一旦找到這方程,因為
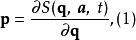 哈密頓-雅可比方程
哈密頓-雅可比方程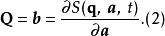 哈密頓-雅可比方程
哈密頓-雅可比方程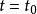 哈密頓-雅可比方程
哈密頓-雅可比方程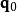 哈密頓-雅可比方程
哈密頓-雅可比方程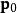 哈密頓-雅可比方程
哈密頓-雅可比方程給予 q與 p在時間 的初始值, 與 ,可以求出運動常數 a, b。知道這兩組運動常數,立刻可以得到舊正則坐標 q與 p隨時間的演變。
2.哈密頓特徵函式
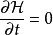 哈密頓-雅可比方程
哈密頓-雅可比方程假設,哈密頓量不顯含時: 。那么,
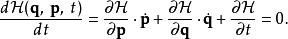 哈密頓-雅可比方程
哈密頓-雅可比方程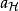 哈密頓-雅可比方程
哈密頓-雅可比方程哈密頓量是一個運動常數,標記為 :
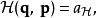 哈密頓-雅可比方程
哈密頓-雅可比方程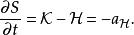 哈密頓-雅可比方程
哈密頓-雅可比方程.
哈密頓主函式可以分離成兩部分:
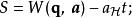 哈密頓-雅可比方程
哈密頓-雅可比方程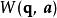 哈密頓-雅可比方程
哈密頓-雅可比方程其中,不含時間的函式 稱為 哈密頓特徵函式。
 哈密頓-雅可比方程
哈密頓-雅可比方程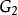 哈密頓-雅可比方程
哈密頓-雅可比方程思考一個新的正則變換。設定哈密頓特徵函式 為一個第二型生成函式 :
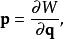 哈密頓-雅可比方程
哈密頓-雅可比方程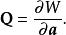 哈密頓-雅可比方程
哈密頓-雅可比方程那么,哈密頓-雅可比方程變為
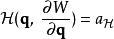 哈密頓-雅可比方程
哈密頓-雅可比方程由於哈密頓特徵函式不顯含時,新舊哈密頓量的關係為
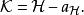 哈密頓-雅可比方程
哈密頓-雅可比方程新正則坐標隨時間的導數變為
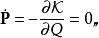 哈密頓-雅可比方程
哈密頓-雅可比方程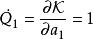 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程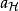 哈密頓-雅可比方程
哈密頓-雅可比方程, 設定 為 ,
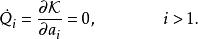 哈密頓-雅可比方程
哈密頓-雅可比方程所以,新正則坐標變為
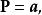 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程 哈密頓-雅可比方程
哈密頓-雅可比方程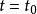 哈密頓-雅可比方程
哈密頓-雅可比方程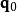 哈密頓-雅可比方程
哈密頓-雅可比方程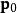 哈密頓-雅可比方程
哈密頓-雅可比方程假若,能找到哈密頓特徵函式 ,給予舊廣義坐標 與舊廣義動量 在時間 的初始值, 與 ,依照前面所述方法,就可以求出舊正則坐標隨時間的演變。
分離變數法
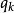 哈密頓-雅可比方程
哈密頓-雅可比方程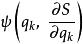 哈密頓-雅可比方程
哈密頓-雅可比方程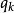 哈密頓-雅可比方程
哈密頓-雅可比方程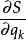 哈密頓-雅可比方程
哈密頓-雅可比方程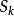 哈密頓-雅可比方程
哈密頓-雅可比方程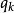 哈密頓-雅可比方程
哈密頓-雅可比方程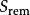 哈密頓-雅可比方程
哈密頓-雅可比方程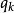 哈密頓-雅可比方程
哈密頓-雅可比方程哈密頓-雅可比方程最有用的時候,是當它可以使用分離變數法,來直接地辨明運動常數。假設,HJE 可以分為兩部分。一部分只跟廣義坐標 、哈密頓主函式的偏導數 有關,標記這部分為。另一部分跟、 無關。對於這狀況,哈密頓主函式 S可以分離為兩個函式。一個函式除了廣義坐標 以外,跟任何其它廣義坐標無關。另外一個函式 跟無關。
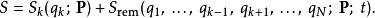 哈密頓-雅可比方程
哈密頓-雅可比方程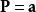 哈密頓-雅可比方程
哈密頓-雅可比方程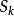 哈密頓-雅可比方程
哈密頓-雅可比方程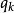 哈密頓-雅可比方程
哈密頓-雅可比方程由於每一個廣義動量都是運動常數,,函式只跟廣義坐標 有關:
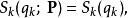 哈密頓-雅可比方程
哈密頓-雅可比方程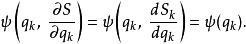 哈密頓-雅可比方程
哈密頓-雅可比方程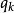 哈密頓-雅可比方程
哈密頓-雅可比方程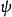 哈密頓-雅可比方程
哈密頓-雅可比方程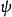 哈密頓-雅可比方程
哈密頓-雅可比方程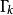 哈密頓-雅可比方程
哈密頓-雅可比方程若將哈密頓主函式 S代入 HJE,則可以觀察到,只出現於函式內部,而不出現於 HJE 的任何其它地方。所以,函式必須等於常數(在這裡標記為)。這樣,可得到一個一階常微分方程:
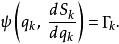 哈密頓-雅可比方程
哈密頓-雅可比方程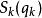 哈密頓-雅可比方程
哈密頓-雅可比方程在某些問題里,很幸運地,函式 S可以完全的分離為 N個函式:
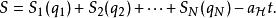 哈密頓-雅可比方程
哈密頓-雅可比方程這些問題的偏微分方程可以分離為 N個常微分方程 。
哈密頓主函式 S的可分性,相關於哈密頓量和廣義坐標的選擇。假若,一個物理系統符合施特克爾條件(Staeckel conditions) ,則哈密頓主函式 S可以完全分離。
