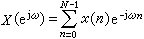周期圖法
正文
一種信號功率譜密度估計方法。它的特點是：為得到功率譜估值，先取信號序列的離散傅立葉變換，然後取其幅頻特性的平方並除以序列長度N，即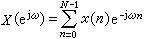
(1)
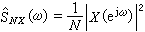(2)
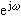)具有周期性，因而這種功率譜
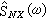也具有周期性，常稱為周期圖。早期的統計學者曾利用這種方法從大量的數據中尋找隱藏的周期性的規律。周期圖是信號功率譜的一個有偏估值；而且，當信號序列的長度增大到無窮時，估值的方差不趨於零。因此，隨著所取的信號序列長度的不同，所得到的周期圖也不同，這種現象稱為隨機起伏。由於隨機起伏大，使用周期圖不能得到比較穩定的估值。一些學者對此作了改進。 為了減小隨機起伏，M.S.巴特利特提出平均周期圖法，即先把信號序列分為若干段，對每段分別計算其周期圖，然後取各個周期圖的平均作為功率譜的估值。平均周期圖可以減小隨機起伏，但是，如果信號序列不是足夠長，由於每段序列長度變短，功率譜估值對不同頻率成分的分辨能力也隨之下降。另一種改進方法是將周期圖與一個適當的頻域窗函式相褶積，從而對周期圖產生平滑作用，以減小隨機起伏。加窗處理的結果雖然可以使隨機起伏減小，但也會使周期圖的分辨能力下降。
P.O.韋爾奇提出一種把加窗處理與平均處理結合起來的方法。先把分段的數據乘以窗函式(進行加窗處理)，分別計算其周期圖，然後進行平均。韋爾奇方法是較常用的一種計算方法。為了得到較好的功率譜估值，加窗和平均處理均應兼顧減小隨機起伏和保證有足夠的譜解析度兩個方面。
周期圖法的優點是能套用離散傅立葉變換的快速算法來進行估值。對利用式(1)、(2)得到的功率譜估值進行傅立葉反變換，可以得到信號的自相關函式估值。這種方法適用於長信號序列的情況，在有足夠的序列長度時，套用改進的周期圖法，可以得到較好的功率譜估值，因而套用很廣。
參考書目
A.V.Oppenheim and R.W.Schafer，Digital SignalProcessing，Prentice-Hall，Inc.,Englewood Cliffs,New Jersey,1975.
