正文
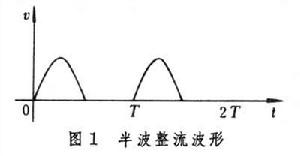
電流(或電壓)按非正弦律作周期變化的電路。例如,一個線性時不變電路,當所接電源提供的電壓具有方波波形或鋸齒波波形時,其內部各處的穩態回響(電壓或電流)便具有按非正弦律作周期變化的波形。又如,常用的整流電路,儘管其輸入是正弦電壓,但因其內部含有非線性元件──半導體整流器,使得其輸出卻是波形如圖1(半波整流)或圖2(全波整流)所示的非正弦電壓。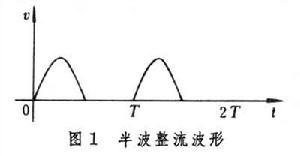 非正弦周期電路
非正弦周期電路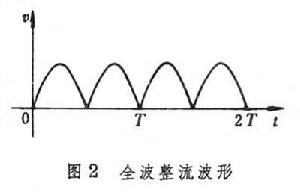 非正弦周期電路
非正弦周期電路按非正弦律作周期變化的電流和電壓稱為非正弦周期電流和電壓,可用周期函式f(t)來表示。
非正弦周期電流(或電壓)的分解 一個周期函式若能滿足狄里赫利條件,便可展成一個無窮的三角級數,即
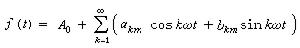 (1)
(1)
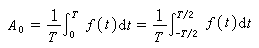 (2)
(2)
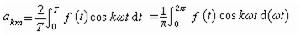 (3)
(3)
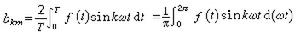 (4)
(4)
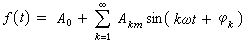 (5)
(5)
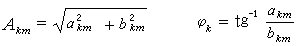
上式是f(t)的另一種表達式。式中第一項A0稱為f(t)的恆定分量(又稱直流分量),第二項A1sin(ωt+φ1)稱為f(t)的基波分量,其餘各項統稱為諧波分量,而且按K=2,3…,分為二次諧波、三次諧波、……。基波分量與原函式f(t)有相同的周期(或頻率),其他諧波的周期則是原函式周期的整數倍,基中凡倍數為奇數者統稱為奇次諧波,為偶數者統稱為偶次諧波。非正弦周期電壓和電流所含等於和大於二次的諧波分量,分別稱為諧波電壓和諧波電流。在電力系統中為保證電能質量需對這些諧波加以抑制(見高次諧波抑制)。
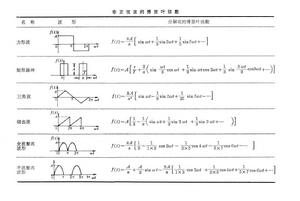
傅立葉級數取無窮多項才能準確代表原函式。但在要求不很高,而級數收斂又較快的情況下,可以把五次以上諧波略去不計。幾種常見的非正弦波的傅立葉級數列於表中。從這些級數中可以看出,近於正弦波的三角波的級數收斂最快。
有效值和平均值 非正弦周期量f(t)的有效值定義為
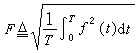
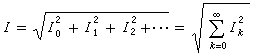 (6)
(6)
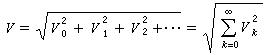 (7)
(7)
非正弦周期電流i 的平均值定義為其絕對值的平均值,即
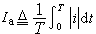 (8)
(8)
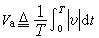 (9)
(9)
平均值與恆定分量是有區別的。一個非正弦周期電流(或電壓)的平均值永不為零,而其恆定分量都可能為零。
非正弦周期電路的穩態分析
在非正弦周期電壓或電流(即激勵)作用下,線性時不變電路的穩態回響可按下列步驟進行計算。
①將給定的非正弦周期電壓或電流分解成傅立葉級數。級數究竟取幾項視要求計算的精度而定,項數確定後,再按式(1)、(2)和(3)算出各個有關傅立葉係數。
②按順序計算級數中各分量單獨作用於電路時所引起的穩態回響。在計算直流分量引起的回響時,應將原電路中的電感器視為短路,電容器視為開路,在計算各次諧波引起的回響時應使用相量法,而且要注意到電感器的感抗XL(XL=KωL)和電容器的容抗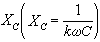
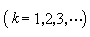 皆與諧波的次數K有關,即它們的數值隨諧波的次數不同而不同。
皆與諧波的次數K有關,即它們的數值隨諧波的次數不同而不同。
③將第二步中求得的對應於各次諧波的穩態回響相量轉換成正弦量,再將這些正弦量與對應於直流分量的回響(是與時間t 無關的常數)疊加,便得出所欲求的穩態回響。
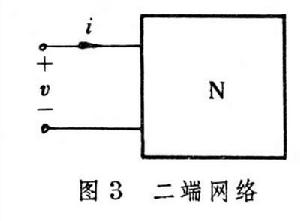 非正弦周期電路
非正弦周期電路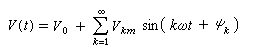
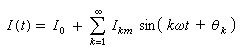
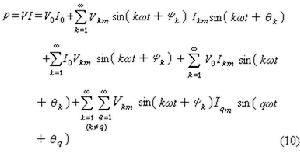
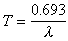
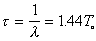 (12)
(12)
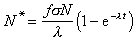 (13)
(13)
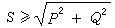 (14)
(14)
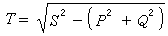 (15)
(15)
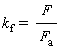 (16)
(16)
畸變因數 用以度量周期信號波形與正弦波的差別的量。以Kd表示。它等於其基波的有效值F1與有效值之比,即
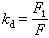
 非正弦周期電路
非正弦周期電路