信號分類
常見的周期信號有:正弦信號、脈衝信號以及它們的整流、微分、積分等。這類可稱為簡單信號。它們的特點是在一個周期內的極值點不會超過兩個且周期性特徵明顯。對於這類已明確具有周期特性的信號,周期與否的判別相對簡單,周期測量的方法也很成熟完善,如:過零檢測法,脈衝整形法等
表達式
x(t)=x(t+kT),k=1,2......
式中t表示時間,T表示周期。
信號劃分
一個信號既可以是模擬的也可以是數字的。如果它是連續時間和連續值,那么它就是一個模擬信號。如果它是離散時間和離散值,那么它就是一種數位訊號。除了這種區分外,信號也可以分為周期性的或非周期性的。周期性信號是一種經過一定時間重複本身的,而非周期性信號則不會重複。模擬和數位訊號既可以是周期性的也可以是非周期性的。
區別周期信號和非周期信號的方法:1、周期信號的頻譜是離散的,準周期信號的頻譜是連續的。2、因周期信號可以用一組整數倍頻率的三角函式表示,所以在頻域裡是離散的頻率點。準周期信號做Fourier變換的時候,n趨向於無窮,所以在頻譜上就變成連續的了。
周期性計算
試判斷下列各信號f(t)是否為周期信號。若是,其周期T為多少?
(1)f(t)=cos2t+sin3t
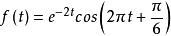 周期信號
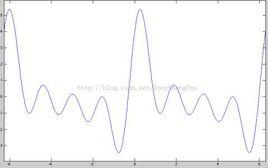
周期信號(2)
(3)f(t)=10cos4πtU(t)
解
(1) f(t)為兩個子信號f(t)=cos2t與f(t)=sin3t的和,即f(t)=f(t)+f(t),且f(t)=f(t-nT),f(t)=f(t-nT),其中n∈ Z,n∈ Z。則當T1/T2=n2/n1(n與n必須為不可約的整數)時,f(t)即為周期信號,其周期T=nT=nT。
今子信號cos2t的周期為πs,子信號sin3t的周期為2π/3s。故有T1/T2=3/2
由於3/2已為不能再約的整數比,故f(t)為周期信號,其周期T為2πs.
(2) 因f(t)的振幅是隨時間按指數規律變化的,故f(t)不是周期信號。
(3) 因f(t)不是無始無終的信號,而是有始無終的信號,故不是周期信號。
matlab程式
在數位訊號處理中,有四種傅立葉變換,如果時域是周期的,則變換域一定是離散(譜線)的。如果頻域具有周期性,則時域一定是離散的。
矩形信頻譜
fs=150;N=200; %採樣頻率為150Hz,點數為200點
Dt=1/fs;%數字角頻率
t=(0:N-1)*Dt;
A=1;P=2*pi;
y=A*square(P*(t+0.05),10); %周期脈衝函式
subplot(2,1,1)
plot(t,y); %周期脈衝波形
axis([0 1.5 0 1.5])
xlabel('時間')
ylabel('幅值')
title('周期矩形脈衝信號')
Y=fft(y); %快速傅立葉變換
fy=(abs(Y)*2)/N; %頻譜
subplot(2,1,2)
stem(fy);
axis([0 30 0 2])
xlabel('頻率')
ylabel('幅值')
title('周期矩形脈衝信號的幅頻譜圖')
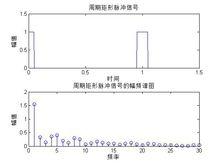 周期信號
周期信號