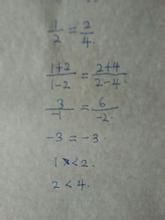合分比定理:合分比定理，如果a/b=c/d（a>b， c>d -百科知識中文網

證明

法一

設：由題設得a/b=c/d=t，那么a=bt,c=dt
a=bt
則a+b=bt+b
a+b=b(t+1)
(b+a)/b=t+1
同理(a-b)/b=t-1
代入，即(a+b)/(a-b)=(t+1)/(t-1)
同理(c+d)/(c-d)=(t+1)/(t-1)
因此(a+b)/(a-b)=(c+d)/(c-d)

法二

(a+b)/(a-b)上下同除以b
則將a/b用c/d替換b/b用d/d替換
上下約分即可得(a+b)/(a-b)=(c+d)/(c-d)

相關定理

合比定理：如果a/b=c/d,那么(a+b)/b=(c+d)/d（b、d≠0）
分比定理：如果a/b=c/d那么(a-b)/b=(c-d)/d（b、d≠0）
合分比定理：如果a/b=c/d那么（a+b)/(a-b)=（c+d)/(c-d)（b、d、a-b、c-d≠0）
等比定理：如果a/b=c/d那么a/c=b/d（a、b、c、d≠0）

合比定理

在一個比例里，第一個比的前後項的和與它後項的比，等於第二個比的前後項的和與它的後項的比，這叫做比例中的合比定理。

分比定理

在一個比例里，第一個比的前後項的差與它的後項的比，等於第二個比的前後項的差與它們的後項的比，這叫做比例中的分比定理。