簡介
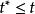合一
合一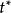
合一 合一
合一 合一
合一 合一 合一 合一 合一 合一在數理邏輯中，特別是套用於計算機科學中，兩個項的同一是就特殊化次序而言的並(格的最小上界),就是說，我們在項的集合上假定一個預序，其中意味著是通過代換(substitute)在中某些項的一個或多個自由變數而從獲得的。和的同一，如果存在的話，是和二者的代換實例的一個項。和的任何公共的代換實例也是的實例。
合一
合一
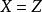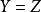合一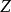
合一
合一例如，對於多項式和可以通過採納和而同一到。
Prolog 中的合一
同一概念是在Prolog背後的主要想法。它表示綁定變數的內容的機制並可以看作為一種只一次的(one-time)賦值。在Prolog中，這種操作用符號"="來指示。
在傳統Prolog中，未實例化的變數—就是說在它上面以前沒有進行合一，可以合一於一個原子、一個項、或另一個未實例化的變數，因此在效果上變成了它的別名。在很多現代Prolog方言和一階邏輯演算中，變數不能合一於包含它的項；這叫做出現檢查。
Prolog原子只能合一於同一個原子。
類似的，項只能合一於另一個項，如果頂部函式符號和項的元數(arity)和這個項是一樣的，並且參數可以同時合一。注意這是遞歸行為。
1.在傳統Prolog中，未實例化的變數—就是說在它上面以前沒有進行合一，可以合一於一個原子、一個項、或另一個未實例化的變數，因此在效果上變成了它的別名。在很多現代Prolog方言和一階邏輯演算中，變數不能合一於包含它的項；這叫做出現檢查。
2.Prolog原子只能合一於同一個原子。
3.類似的，項只能合一於另一個項，如果頂部函式符號和項的元數(arity)和這個項是一樣的，並且參數可以同時合一。注意這是遞歸行為。
合一由於它的聲明本性，一序列合一的次序(通常)是不重要的。
注意在一階邏輯的術語中，原子是基本命題而且其合一同Prolog項一樣。
合一的例子
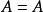合一:成功(重言式)
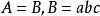合一
合一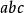
合一
合一:和二者合一於原子
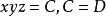合一:合一是對稱的
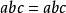合一:合一成功
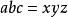合一:合一失敗，因為原子是不同的
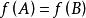合一 合一 合一:合一於
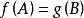合一:失敗，因為項的頭部是不同的
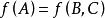合一:合一失敗，因為項有不同的元數
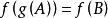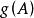合一 合一
合一:合一於項
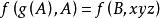合一 合一
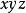合一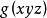 合一
合一:合一於原子而合一於項
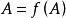合一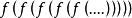 合一
合一:無限合一，合一於。在嚴格的一階邏輯和很多現代Prolog方言中，這是禁止的(並由出現檢查來強制)
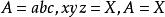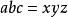合一 合一:合一失敗；效果上
