定義
可測空間
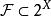 可測空間
可測空間 可測空間
可測空間 可測空間
可測空間 可測空間
可測空間 可測空間
可測空間定義1 設X是一個非空集, 是X的一個σ代數,稱(X, )為一個 可測空間。每個集合A∈ 是(X, )中的可測集,也稱為X中的 可測集,簡稱 可測集。
 可測空間
可測空間 可測空間
可測空間例如,當 是R中的波萊爾集類B 時,(R,B)稱為波萊爾可測空間;當 是R中的勒貝格可測集類L時,(R,L)稱為勒貝格可測空間。
註:1.可測空間是測度的定義域,在一個可測空間上可以定義不止一種測度。
 可測空間
可測空間2.若集函式 具有以下性質:
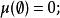 可測空間
可測空間(1)
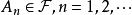 可測空間
可測空間(2)若 互不相交,有
 可測空間
可測空間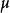 可測空間
可測空間 可測空間
可測空間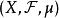 可測空間
可測空間則稱 為(X, )上的一個 測度,稱三元組 為 測度空間。
性質
 可測空間
可測空間 可測空間
可測空間 可測空間
可測空間 可測空間
可測空間 可測空間
可測空間 可測空間
可測空間設 (E, ) 與 (E′, ′) 為兩個可測空間.,稱從E到E′中的映射f 是 ( , ′) 可測的。 或更簡單地說,f 是可測的,如果E′ 的任一可測子集經f 的逆象是E的可測子集。兩個可測映射的合成仍是可測的映射。為使映射f 可測,只須對生成σ-代數 ′ 的 ′之子集的任一元 素A′,其經由f 的逆象可測。
 可測空間
可測空間如果E′是拓撲空間,且 ′是E′的波雷爾σ-代數,為使從E到E′中的映射f 可測,只須E′的任一開集經由f 的逆象可測。當E′為可分度量空間時,為使f 可測,只須E′的任一開球經由f 的逆象可測。
當E與E′為賦以它們的波雷爾σ-代數的拓撲空間時,從E到E′中的任一連續映射都是可測的。
