可測矩形

C作為空間Ω1×Ω2上的集類，其中的元素稱為可測矩形（measurable rectangle）。

簡介

乘積空間

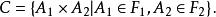可測矩形

設(Ω,)及(Ω,)是兩個可測空間，令 由C作為空間Ω×Ω上的集類所生成的σ代數σ(C)稱為與的乘積σ代數，以×表示，而稱(Ω×Ω,×)為(Ω,)與(Ω,)的乘積空間。

定義

C中的元素稱為可測矩形，σ(C)=(×)中的元素稱為乘積空間中的可測集。

可測空間

可測空間(measurable space)是測度論中的基本概念，可測空間和定義在可測空間上的測度構成測度空間。可測空間是測度的定義域，在一個可測空間上可以定義不止一種測度。

可測矩形

可測矩形

可測矩形

可測矩形

可測矩形

設X是一個非空集， 是X的一個σ代數，稱（X， ）為一個 可測空間。每個集合A∈ 是（X， ）中的可測集，也稱為X中的 可測集，簡稱 可測集。