定義
(X,Σ)是一個可測空間,並且B是域 K(通常是實數空間 R或複數空間 C)上的巴拿赫空間,如果函式f:X→B滿足如下條件,對於任意連續線性泛函g:B→ K,函式
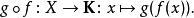 弱可測函式
弱可測函式是關於Σ和 K上一般的波萊爾σ代數的可測函式,則f被稱為是 弱可測的。
機率空間上的可測函式通常被稱為隨機變數(或隨機向量,如果它在例如巴拿赫空間B的向量空間中取值)。因此,作為上述定義的特殊情形,如果(Ω,Σ, P)是一個機率空間,如果函式Z:Ω→B滿足,對於任意連續線性泛函g:B→ K,函式
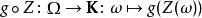 弱可測函式
弱可測函式是在一般意義下的關於Σ和 K上一般的波萊爾σ代數的 K值隨機變數(即可測函式),則函式Z被稱為(B值) 弱隨機變數(或 弱隨機向量)。
性質
可測性和弱可測性之間的關係由如下給出,被稱為 Pettis定理或 Pettis可測性定理。
如果存在子集N⊆X有測度μ(N)=0使得f(X\N)⊆B是可分的,則函式f被稱為幾乎必然 可分值的(或 本性可分值的)。
定理(Pettis):一個函式f:X→B定義在在測度空間(X,Σ,μ)上在巴拿赫空間B中取值,它是(強)可測的(關於Σ上的波萊爾σ代數)若且唯若它是弱可測的且幾乎必然可分值的。
在B可分的情形下,由於可分巴拿赫空間的任何子集本身是可分的,所以可以取上述N為空集,由此可知當B可分時弱可測性和強可測性的概念一致。
參見
•博赫納可測函式
•博赫納積分
•佩蒂斯積分
•向量值測度
