基本介紹
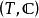 可測集值映射
可測集值映射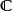 可測集值映射
可測集值映射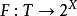 可測集值映射
可測集值映射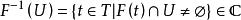 可測集值映射
可測集值映射設 是可測空間,其中T為某個集合, 為T中的可測子集族,X為拓撲空間, 為集值映射,若對於X中每一開集U, ,則稱集值映射F為 可測的。可測集值映射也稱為 集值隨機變數或 隨機集。
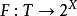 可測集值映射
可測集值映射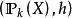 可測集值映射
可測集值映射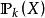 可測集值映射
可測集值映射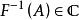 可測集值映射
可測集值映射當X是可分度量空間,且 具非空緊值時,集值映射F是可測的若且唯若F作為從T到 中的單值映射是可測的(其中 表示X的一切緊子集所成之族,h為豪斯多夫度量),它等價於:對X中每個閉集A,
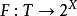 可測集值映射
可測集值映射當(X,d)是可分度量空間,且 具非空完備值時,F的可測性等價於下述條件之一:
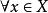 可測集值映射
可測集值映射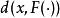 可測集值映射
可測集值映射1. ,函式 是可測的。
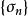 可測集值映射
可測集值映射2.F有一列可測單值選擇 使得
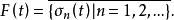 可測集值映射
可測集值映射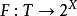 可測集值映射
可測集值映射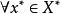 可測集值映射
可測集值映射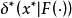 可測集值映射
可測集值映射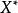 可測集值映射
可測集值映射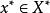 可測集值映射
可測集值映射當X是局部凸可度量化可分向量空間,且具非空緊凸值時,F的可測性也等價於:,支撐函式是可測的,其中為X的對偶空間,對於與A⊂X ,
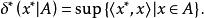 可測集值映射
可測集值映射相關定義及定理
 可測集值映射
可測集值映射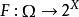 可測集值映射
可測集值映射定義1設為可測空間,X為拓撲空間,B(X)為X上的Borel代數。對集值映射,記F的圖
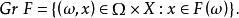 可測集值映射
可測集值映射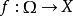 可測集值映射
可測集值映射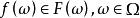 可測集值映射
可測集值映射 可測集值映射
可測集值映射若有可測映射使得,則稱為F的可測選擇。
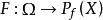 可測集值映射
可測集值映射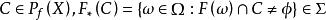 可測集值映射
可測集值映射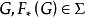 可測集值映射
可測集值映射定義2 稱集值映射為強可測的,若任給;稱F為 可測的,若任給開集。
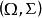 可測集值映射
可測集值映射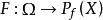 可測集值映射
可測集值映射定理1 設為可測空間,(X,d)為可分度量空間,為閉集值映射。考慮下列情況:
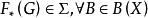 可測集值映射
可測集值映射(1);
(2) F為強可測的;
(3)F為可測的;
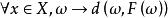 可測集值映射
可測集值映射(4)為可測函式;
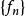 可測集值映射
可測集值映射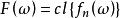 可測集值映射
可測集值映射(5)(Castaing表示)存在一列F的可測選擇使得;
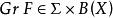 可測集值映射
可測集值映射(6) F為圖象可測的,即:。
那么我們有如下結論:
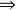 可測集值映射
可測集值映射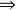 可測集值映射
可測集值映射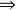 可測集值映射
可測集值映射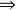 可測集值映射
可測集值映射(i) (1)(2)(3)(4)(6);
 可測集值映射
可測集值映射(ii)當X還是完備的(即x是Polish空間)時,(3)(5);
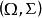 可測集值映射
可測集值映射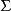 可測集值映射
可測集值映射(iii)當X是Polish空間,為完備的可測空間,即上
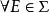 可測集值映射
可測集值映射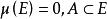 可測集值映射
可測集值映射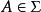 可測集值映射
可測集值映射存在一σ-有限的完備測度μ(即,若,則),則(1)~(6)全部等價。
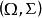 可測集值映射
可測集值映射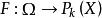 可測集值映射
可測集值映射定理2為可測空間,X為可分度量空間,為集值映射.則下列命題等價
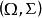 可測集值映射
可測集值映射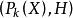 可測集值映射
可測集值映射(1) F為到度量空間的可測映射;
(2) F為強可測的;
(3) F為可測的。
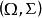 可測集值映射
可測集值映射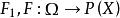 可測集值映射
可測集值映射定理3為可測空間,X為可分Banach空間,為可測集值映射,則
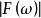 可測集值映射
可測集值映射(1)可測;
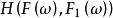 可測集值映射
可測集值映射(2)可測;
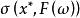 可測集值映射
可測集值映射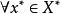 可測集值映射
可測集值映射(3)可測,。

