定義
可測映射
可測映射
可測映射
可測映射
可測映射
可測映射
可測映射 可測映射
可測映射設 和 是兩個可測空間， 是 的映射（簡記為： ）。如果對於一切 ，有 ，則稱 是 可測映射。
可測映射
可測映射
可測映射 可測映射註：有些地方用 表示集類 ，用 表示 可測映射。
相關定義：
可測映射
可測映射
可測映射
可測映射 可測映射
可測映射
可測映射 可測映射 可測映射
可測映射
可測映射 可測映射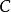 可測映射 可測映射
可測映射
可測映射設
是實數域，，和分別表示及上的 Borel代數，令是一可測空間，是的映射。如果，則稱是 Borel 可測函式，簡稱可測函式。若進一步只取實數，則稱為實值可測函式。設為複數域，則稱為復值可測函式。性質
性質1
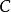可測映射 可測映射 可測映射 可測映射 可測映射 可測映射
可測映射設 和 是兩個可測空間， 為生成 代數的一集類。若 是 的映射，使得 成立，則f為可測映射 。
性質2
可測映射 可測映射 可測映射設 為可測空間 上的一個數值函式，即取值於 ，則下列條件等價：
可測映射(1) 為可測函式
可測映射(2)
可測映射(3)
可測映射(4)
可測映射(5)
性質3
可測映射上實值（復值）可測函式全體構成實域（復域）上的一向量空間 。
性質4
可測映射 可測映射設 都為 上的可測函式：
可測映射(1) 為可測函式
(2) 若 處處有意義，則 為可測函式
可測映射 可測映射(3)若 處處有意義，則 為可測函式
