簡介
給定兩個測度空間Ω和Ω,映射f:Ω→Ω稱為從Ω到Ω的 可測變換。是從一個測度空間到另一個測度空間之間的一個映射。設f是從Ω到Ω的 可測變換,且f是雙射,則稱f為從Ω到Ω的 雙可測變換。
概念
可測變換亦稱可測映射,是可測函式概念的推廣,主要用於抽象積分的變數變換。設(Ω,F)和(Ω,F)是兩個可測空間,f是Ω到Ω中的映射。如果(Ω,F)中每個可測集A的原像f (A)均是(Ω,F)中的可測集,那么f稱為Ω到Ω的可測映射。若f是可測空間(Ω,F)上的實值函式,則f在(Ω,F)上可測的充分必要條件是f為(Ω,F)到(R ,B )中的可測映射,其中R為實數空間,B為波萊爾集類。若f是可測空間(Ω,F)上的擴充實值函式,則f在(Ω,F)上可測的充分必要條件是f為(Ω,F)到(R,B)中的可測映射,其中R為擴充實數空間,B為廣義波萊爾集類。若f是測度空間(Ω,F,μ)到可測空間(Ω′,C)的可測映射,g是(Ω′,C)上的可積函式,則:
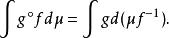 可測變換
可測變換又若A∈C,則:
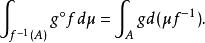 可測變換
可測變換測度論
亦稱抽象測度論或抽象積分論,研究一般集合上的測度和積分的理論。是勒貝格測度和勒貝格積分理論的進一步抽象和發展。
測度是集合的一種度量,它是長度、面積、體積概念的推廣。首先試圖把長度、面積、體積概念推廣到任意點集而得出一般的“測度”觀念的是杜·布瓦-雷蒙( P.D.G.Du Bois-Reymond),他在《一般函式論》(1882年)中提出容量概念,即測度概念的雛形。隨後漢克爾(H.Hankel)、施托爾茨(O.Stolz)、哈納克(C.G.A.Harnack)、康托爾(G.(F.P.).Cantor)等人發展了這種思想,其中康托爾於1884年對直線上的有界集A定義它的測度μ(A):首先對任意正數δ,令:
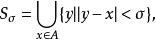 可測變換
可測變換μ(S)代表S的長度;再令:
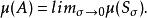 可測變換
可測變換康托爾給出的測度不具有可加性。例如,設Q為有理數全體,A=[0,1]∩Q,B=[0,1]\A,則[0,1]=A∪B,μ(A)=μ(B)=1,μ([0,1])=1,但μ([0,1])≠μ(A)+μ(B),因而很不合理。
佩亞諾(G.Peano)於1887年引入了平面有界集A的內、外測度的概念:包含A的多邊形面積的下確界稱為A的外測度,含於A內的多邊形面積的上確界稱為A的內測度。若A的內、外測度相等,則這個公共值稱為A的測度,並稱A為可測集。佩亞諾證明了:
1.A可測的充分必要條件是A的邊界的外測度為0。
2.若f(x)是定義在[a,b]上的有界正函式,A={(x,y)|a≤x≤b,0≤y≤f(x)},則f(x)的黎曼下積分為A的內測度,黎曼上積分為A的外測度,f(x)黎曼可積若且唯若A是可測集。
3.測度具有有限可加性。
若爾當(M.E.C.Jordan,)於1892年在R中發展了佩亞諾可測集的概念。原來定義外測度時,要用多邊形去覆蓋點集,他規範為用有限個開區間去覆蓋,其餘不變.若爾當的改進使測度概念前進了一大步,蘊涵了勒貝格測度的萌芽,但仍有明顯的缺點。主要是它仍只具有有限可加性,從而導致有些簡單的點集也不可測。例如,令A=[0,1]∩Q,則A的若爾當內測度為0,而外測度為1,因而A在若爾當意義下不可測。總之,若爾當測度只適合於黎曼積分的需要。波萊爾((F.-É.-J.-)É.Borel)於1898年,先由開集經過可列並與余的運算導致一類集,即所謂波萊爾集類。再對每個有界波萊爾集對應一個實數,即波萊爾測度,並使得這種測度具有可列可加性。波萊爾的這種思想對測度理論做出了重大貢獻,成為近代測度論中用公理方式引出σ代數概念的起源,並為勒貝格(H.L.Lebesgue)的工作開闢了道路。波萊爾的學生勒貝格在前人工作的基礎上,於1902年以更一般的形式建立起比較完善的測度理論.他在定義點集測度的方法上,容許可列覆蓋,使所建立的測度具有可列可加性,並且相當廣泛的一類點集的測度有了定義。勒貝格測度是現代抽象測度的起源,在它的基礎上建立的勒貝格積分,是現代分析中套用最廣和意義重大的積分。卡拉西奧多里(C.Carathéodory)於1914年發展了外測度理論,對測度進行了公理化研究,並給出了測度擴張的典型方法,成為近代測度論的基礎.拉東(J.Radon)、薩克斯(S.Saks)、弗雷歇(M.-R.Fréchet)以及另外一些人考慮了一般集合上的測度以及測度空間的乘積,並建立了一般可測集上積分的理論。
一般集合上的測度和積分理論是最廣泛的測度理論,但為適應各方面的需要,還出現了其他種種特殊的測度和積分。例如,20世紀30年代初,伴隨著人們對取值於巴拿赫空間的函式性質特別是可微性和可積性的研究,出現了有關向量值測度的一些工作。1960年以後,向量值測度理論得到蓬勃發展,並逐漸趨於完善。又如,19世紀建立的傅立葉分析理論,對於套用數學而言,當時已是令人滿意的數學工具,但由於黎曼積分的局限性,對於函式與展開式之間的關係,直到勒貝格積分理論確立之後才有深刻的揭示.勒貝格積分的出現對於傅立葉展開的研究顯然促進了一大步,但依舊顯示出了它的局限性.研究拓撲群上的測度是建立群上傅立葉分析的基本問題之一,這個問題自1930年以來,經過哈爾(Haar,A.)、韋伊(A.Weil)和蓋爾范德(И.М.Гельфанд)等人的工作而趨於完善.再如,20世紀初測度論的建立,使得人們對R中的子集關於n維勒貝格測度的性質有了很好的了解。但在處理與R中低維點集有關的數學問題時遇到了困難。在這種背景下,20世紀20年代出現了幾何測度論,它是研究高維空間中低維點集的測度及低維點集上積分的理論。
測度概念與積分概念緊密相關。每一種測度理論的推廣都可導致一種積分理論的推廣。測度理論不僅是積分理論的基礎,而且在現代分析以及機率論等許多數學領域中也有著廣泛的套用。
可測函式
分析學中討論得最廣的函式類。它有許多等價的定義方式,這裡採用如下定義:設(Ω,F)為可測空間,f(x)是定義在Ω上的實值(或擴充實值)函式。若對任意實數c,恆有{x|f(x)>c}∈F,則f(x)稱為(Ω,F)中的可測函式或Ω上的F可測函式。在這個定義中,條件f(x)>c可用f(x)≥c,f(x)<c,f(x)≤c中任一條件來替代.當F為與特殊的測度相應的可測集類時,相應的可測函式可以冠以這些測度的名稱。例如說f(x)為波萊爾可測函式、勒貝格可測函式等。f(x)在(Ω,F)上可測的充分必要條件是,對於直線上的任何波萊爾集M,f(M)是可測集,即f(M)∈F。勒貝格可測函式的概念是由勒貝格(H.L.Lebesgue)於1902年引入的,拉東(J.Radon)於1913年把它推廣到一般的可測空間。除一些涉及R中的特殊拓撲性質(如盧津定理)外,可測空間中的可測函式的性質與勒貝格可測函式的性質基本相同。例如,可測函式類對於四則運算封閉,對於極限運算封閉,幾乎處處收斂的可測函式列是近於一致收斂的,也即葉戈羅夫定理成立。
可測空間
測度的定義域,測度論中的基本概念。設F是基本空間Ω上的σ代數,稱(Ω,F)為可測空間,而稱F中的元素A是(Ω,F)中的可測集,也稱為Ω中的F可測集,簡稱可測集。例如,當F是R中的波萊爾集類B時,(R,B)稱為波萊爾可測空間。當F是R中的勒貝格可測集類L時,(R,L)稱為勒貝格可測空間。可測空間是測度的定義域,在一個可測空間上可以定義不止一種測度。
