可微函式

在微積分學中，可微函式是指那些在定義域中所有點都存在導數的函式。可微函式的圖像在定義域內的每一點上必存在非垂直切線。因此，可微函式的圖像是相對光滑的，沒有間斷點、尖點或任何有垂直切線的點。 一般來說，若是函式ƒ定義域上的一點，且ƒ′()有定義，則稱ƒ在點可微。這就是說ƒ的圖像在(, ƒ())點有非垂直切線，且該點不是間斷點、尖點。

可微性

魏爾斯特拉斯函式連續，但在任一點都不可微。

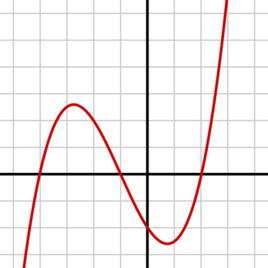
若ƒ在 X點可微，則ƒ在該點必連續。特別的，所有可微函式在其定義域內任一點必連續。逆命題則不成立：一個連續函式未必可微。比如，一個有折點、尖點或垂直切線的函式可能是連續的，但在異常點不可微。

實踐中運用的函式大多在所有點可微，或幾乎處處可微。但斯特凡·巴拿赫聲稱可微函式在所有函式構成的集合中卻是少數。 這表示可微函式在連續函式中不具代表性。人們發現的第一個處處連續但處處不可微的函式是魏爾斯特拉斯函式。

連續可微分類

函式 f是連續可微（continuously differentiable），如果導數 f'(x)存在且是連續函式。

連續可微函式被稱作 classC。一個函式稱作 classC如果函式的一階、二階導數存在且連續。更一般的，一個函式稱作 classC如果前 k階導數 f′( x), f″( x), ..., f( x) 都存在且連續。如果對於所有正整數n，f存在，這個函式被稱為光滑函式或稱 classC。

多元函式

如果一個函式的所有偏導數在某點的鄰域記憶體在且連續，那么該函式在該點可微，而且是class C。(這是可微的一個充分不必要條件)

形式上，一個多元實值函式 f: R→ R在點 x處可微，如果存線上性映射 J: R→ R滿足

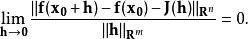可微函式

注意，偏導數都存在並不能保證函式在該點可微。