複合函式的求導法則
設函式
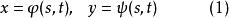複合函式微分法
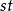複合函式微分法
複合函式微分法定義在 平面的區域 上，函式
複合函式微分法
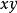複合函式微分法
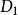複合函式微分法定義在 平面的區域 上，且
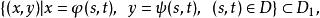複合函式微分法則函式
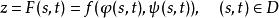複合函式微分法
複合函式微分法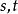
複合函式微分法
複合函式微分法 複合函式微分法是以（2）為外函式，（1）為內函式的複合函式。其中 稱為函式 的中間變數， 為 的自變數 。
定理1
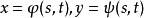複合函式微分法
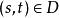複合函式微分法
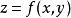複合函式微分法
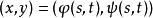複合函式微分法若函式 在點 可微， 在點 可微，則複合函式
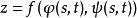複合函式微分法
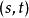複合函式微分法
複合函式微分法
複合函式微分法在點 可微，且它關於 與 的偏導數分別為
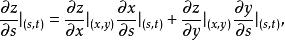複合函式微分法
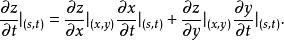複合函式微分法上述兩個公式也稱為鏈式法則。
注意
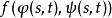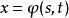複合函式微分法 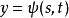複合函式微分法 複合函式微分法
複合函式微分法
複合函式微分法 複合函式微分法 複合函式微分法
複合函式微分法如果只是求複合函式 關於 或 的偏導數，則定理1中 和 只需具有關於 或 的偏導數就夠了。但是對外函式 的可微性假設是不能省略的，否則上述複合函式求導公式不一定成立。如函式
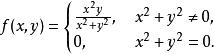複合函式微分法
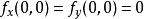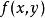複合函式微分法
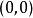複合函式微分法
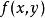複合函式微分法 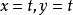複合函式微分法
複合函式微分法 複合函式微分法直接計算可知 ，但 在 處不可微。若以 為外函式， 為內函式，則得以 為自變數的複合函式
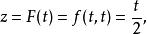複合函式微分法
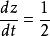複合函式微分法所以 。這是若用鏈式法則，將得出錯誤的結果
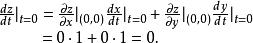複合函式微分法 複合函式微分法這個例子說明在使用複合函式求導公式時，必須注意外函式 可微這一重要條件。
複合函式的全微分
複合函式微分法
複合函式微分法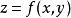 複合函式微分法若以 和 為自變數的函式 可微，則其全微分為
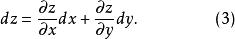複合函式微分法 複合函式微分法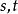 複合函式微分法如果 作為中間變數又是自變數 的可微函式
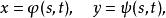複合函式微分法 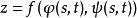複合函式微分法則由定理1知道，複合函式 是可微的，其全微分為
複合函式微分法 複合函式微分法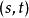 複合函式微分法由於 又是 的可微函式，因此同時有
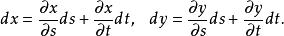複合函式微分法