單元乘法表
單元乘法表如下：
× 1 e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14 e15
1 1 e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14 e15
e1 e1 -1 e3 -e2 e5 -e4 -e7 e6 e9 -e8 -e11 e10 -e13 e12 e15 -e14
e2 e2 -e3 -1 e1 e6 e7 -e4 -e5 e10 e11 -e8 -e9 -e14 -e15 e12 e13
e3 e3 e2 -e1 -1 e7 -e6 e5 -e4 e11 -e10 e9 -e8 -e15 e14 -e13 e12
e4 e4 -e5 -e6 -e7 -1 e1 e2 e3 e12 e13 e14 e15 -e8 -e9 -e10 -e11
e5 e5 e4 -e7 e6 -e1 -1 -e3 e2 e13 -e12 e15 -e14 e9 -e8 e11 -e10
e6 e6 e7 e4 -e5 -e2 e3 -1 -e1 e14 -e15 -e12 e13 e10 -e11 -e8 e9
e7 e7 -e6 e5 e4 -e3 -e2 e1 -1 e15 e14 -e13 -e12 e11 e10 -e9 -e8
e8 e8 -e9 -e10 -e11 -e12 -e13 -e14 -e15 -1 e1 e2 e3 e4 e5 e6 e7
e9 e9 e8 -e11 e10 -e13 e12 e15 -e14 -e1 -1 -e3 e2 -e5 e4 e7 -e6
e10 e10 e11 e8 -e9 -e14 -e15 e12 e13 -e2 e3 -1 -e1 -e6 -e7 e4 e5
e11 e11 -e10 e9 e8 -e15 e14 -e13 e12 -e3 -e2 e1 -1 -e7 e6 -e5 e4
e12 e12 e13 e14 e15 e8 -e9 -e10 -e11 -e4 e5 e6 e7 -1 -e1 -e2 -e3
e13 e13 -e12 e15 -e14 e9 e8 e11 -e10 -e5 -e4 e7 -e6 e1 -1 e3 -e2
e14 e14 -e15 -e12 e13 e10 -e11 e8 e9 -e6 -e7 -e4 e5 e2 -e3 -1 e1
e15 e15 e14 -e13 -e12 e11 e10 -e9 e8 -e7 e6 -e5 -e4 e3 e2 -e1 -1
十六元數的矩陣表示
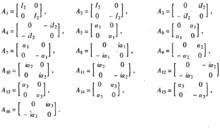矩陣表示
矩陣
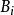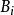十六元數 十六元數如圖所示，可以證明B1,B2...,B16,·為Γ的一組基,並且可以證明 =（1,2,3,……,16)中彼此不同的任意四個元素均可以作為生成元,生成與 =(1,2,...,16)同構的十六個元數的實矩陣表示形式,因此如上B1,B2...,B16,便可以得到Γ的一個實矩陣實現 .
十六元數的性質
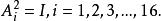十六元數定理1
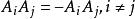十六元數
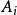十六元數定理2
,j=1,2,…,16.定理3的跡為零，i=1,2,…,16.
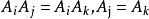十六元數定理4 ,其中i,j,k=1,2,…,16.
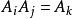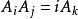十六元數
十六元數定理5 或者 i,j,k=1,2,…,16.
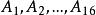十六元數定理6 為線性無關的.
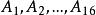十六元數定理7 任一4階矩陣。均可表為 的線性和;
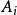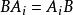十六元數
十六元數定理8如果矩陣B與任一 均滿足乘法交換律,即 (i=1,2,...,16),那么B=kI .
結論
總之，1×任意一個元數ex=這個元數ex，任意一個元數ex×1=這個元數ex，任意一個元數ex的平方都等於－1（除了1以外）
