計算公式
圓周長
圓周長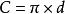
圓周長
圓周長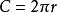
圓周長在古代，這個問題幾乎是依賴於對實驗的歸納。人們在經驗中發現圓的周長與直徑有著一個常數的比，並把這個常數叫做圓周率（西方記做）。於是自然地，圓周長就是：或者（其中是圓的直徑，是圓的半徑）。
圓周率
圓周長後來的數學家們就想辦法算出這個π的具體值，數學家劉徽用的是“割圓術”的方法，也就是用圓的內接正多邊形和外切正多邊形的周長逼近圓周長，求得圓接近192邊型，求得圓周率大約是3.14。
割圓術的大致方法在中學的數學教材上就有。然而必須看到，它很大程度上只是計算圓周率的方法，而圓周長是C = π * d似乎已經是事實了，這一方法僅僅是定出π的值來。仔細想想就知道這樣做有問題，因為他們並沒有從邏輯上證明圓的周長確實正比於直徑，更進一步說他們甚至對周長的概念也僅是直觀上的、非理性的。
推導過程
真正從理論上嚴密推導圓的周長必須依賴近代的分析數學，包括微積分的使用才行。
推導圓周長最簡潔的辦法是用積分。
在平面直角坐標下圓的方程是：
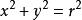圓周長這可以寫成參數方程：
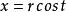圓周長y = r * Sin t
t∈[0, 2π]
於是圓周長就是
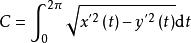圓周長結果自然就是
C = 2π * r
（註：三角函式一般的定義是依賴於圓的周長或面積的，為了避免邏輯上的循環論證，可以把三角函式按收斂的冪級數或積分來定義而不依賴於幾何，此時圓周率就不是由圓定義的常數，而是由三角函式周期性得到的常數）
如果不需要更多的理論討論，上面的做法就足夠了。當然更確切地，人們或許還需要知道在數學上曲線的周長是如何定義的，以及圓的周長的存在性問題。這裡就一時之間說不清了。
