相關研究
其一
 化圓為方
化圓為方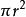 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方方圓的問題與提洛斯問題是同時代的,由希臘人開始研究。有名的阿基米德把這問題化成下述的形式:已知一圓的半徑是r,圓周就是,面積是。由此若能作一個直角三角形,其夾直角的兩邊長分別為已知圓的周長 及半徑,則這三角形的面積就是:
 化圓為方
化圓為方與已知圓的面積相等。由這個直角三角形不難作出同面積的正方形來。但是如何作這直角三角形的邊。即如何作一線段使其長等於一已知圓的周長,這問題阿基米德可就解不出了。
二千年間,儘管對化圓為方問題上的研究 沒有成功,但卻發現了一些特殊曲線。希臘安提豐(公元前430)為解決此問題而提出的 「窮竭法」,是近代極限論的雛形。大意是指先作圓內接正方形(或正6邊形),然後每次 將邊數加倍,得內接8、16、32、…邊形,他相信「最後」的正多邊形必與圓周重合, 這樣就可以化圓為方了。雖然結論是錯誤的,但卻提供了求圓面積的近似方法,成為阿基米德計算圓周率方法的先導,與中國劉徽的割圓術不謀而合,對窮竭法等科學方法的建立產生 直接影響。
其二
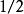 化圓為方
化圓為方 化圓為方
化圓為方其實,若不受標尺的限制,化圓為方問題並非難事,歐洲文藝復興時代的大師義大利數學家達文西(1452-1519)用已知圓為底,圓半徑的為高的圓柱,在平面上滾動一周,所得的矩形,其面積恰為圓的面積,所以所得矩形的面積 ,然後再將矩形化為等積的正方形即可。
現已證明,在尺規作圖的條件下,此題無解。
歷史
公元前5世紀,古希臘哲學家阿那克薩哥拉因為發現太陽是個大火球,而不是阿波羅神,犯有“褻瀆神靈罪”而被投入監獄。在法庭上,阿那克薩哥拉申訴道:“哪有什麼太陽神阿波羅啊!那個光耀奪目的大球,只不過是一塊火熱的石頭,大概有伯羅奔尼撒半島那么大;再說,那個夜晚發出清光,晶瑩透亮象一面大鏡子的月亮,它本身並不發光,全是靠了太陽的照射,它才有了光亮。”結果他被判處死刑。
在等待執行的日子了,夜晚,阿那克薩哥拉睡不著。圓圓的月亮透過正方形的鐵窗照進牢房,他對方鐵窗和圓月亮產生了興趣。他不斷變換觀察的位置,一會兒看見圓比正方形大,一會兒看見正方形比圓大。最後他說:“好了,就算兩個圖形面積一樣大好了。”
阿那克薩哥拉把“求作一個正方形,使它的面積等於已知的圓面積”作為一個尺規作圖問題來研究。起初他認為這個問題很容易解決,誰料想他把所有的時間都用上,也一無所獲。
經過好朋友、政治家伯里克利的多方營救,阿那克薩哥拉獲釋出獄。他把自己在監獄中想到的問題公布出來,許多數學家對這個問題很感興趣,都想解決,可是一個也沒有成功。這就是著名的“化圓為方”問題。
 圖1.希波克拉底證明
圖1.希波克拉底證明2000年前的希波克拉底證明了新月形面積,即左圖:
 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方(半圓)S(扇形),故(新月形)(三角形)。
三角形不難平方化,從而新月形也能平方化。他的方法既簡單又高明,這使得人們充滿希望。直到林德曼證明了圓周率是超越數以後,才知道是不可能的。
問題敘述
化圓為方問題的完整敘述是 :
給定一個圓,是否能夠通過以上說明的五種基本步驟,於有限次內作出一個正方形,使得它的面積等於圓的面積
 化圓為方
化圓為方如果將圓的半徑定為單位長度,則化圓為方問題的實質是作出長度為單位長度倍的線段。
不可能性證明
尺規作圖三大難題提出後,有許多基於平面幾何的論證和嘗試,但在十九世紀以前,一直沒有完整的解答。沒有人能夠給出化圓為方問題的解法,但開始懷疑其可能性的人之中,也沒有人能夠證明這樣的解法一定不存在。直到十九世紀後,伽羅瓦和阿貝爾開創了以群論來討論有理係數多項式方程之解的方法,人們才認識到這三個問題的本質 。
1.尺規可作性和規矩數
 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方在研究各種尺規作圖問題的時候,數學家們留意到,能否用尺規作出特定的圖形或目標,本質是能否作出符合的長度。引進直角坐標系和解析幾何以後,又可以將長度解釋為坐標。比如說,作出一個圓,實際上是作出圓心的位置(坐標)和半徑的長度。作出特定的某個交點或某條直線,實際上是找出它們的坐標、斜率和截距。為此,數學家引入了尺規可作性這一概念。假設平面上有兩個已知的點 和 ,以 為單位長度,射線 為 -軸正向可以為平面建立一個標準直角坐標系,平面中的點可以用橫坐標和縱坐標表示,整個平面可以等價於。
 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方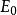 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方設E是的一個非空子集。如果某直線經過 中不同的兩點,就說是 -尺規可作的,簡稱 -可作。同樣地,如果某個圓的圓心和圓上的某個點是 中的元素,就說是 -可作的。進一步地說,如果里的某個點 是某兩個 -可作的直線或圓的交點(直線-直線、直線-圓以及圓-圓),就說點是-可作的。這樣的定義是基於五個基本步驟得來的,包括了尺規作圖中從已知條件得到新元素的五種基本方法。如果將所有-尺規可作的點的集合記作 ,那么當E中包含超過兩個點的時候, 肯定是 的真子集。從某個點集開始,經過一步能作出的點構成集合 ,經過兩步能作出的點就是 ,……以此類推,經過n步能作出的點集就是。而所有從E能尺規作出的點集就是:
 化圓為方
化圓為方另一個與尺規可作性相關的概念是規矩數。設H是從集合 開始,尺規可作點的集合: 那么規矩數定義為H中的點的橫坐標和縱坐標表示的數。
 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方定義:實數和是規矩數若且唯若 是 中的一個點。
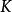 化圓為方
化圓為方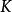 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方可以證明,有理數集是所有規矩數構成的集合 的子集,而又是實數集的子集。另外,為了在複數集內討論問題,也會將平面看作複平面,同時定義一個複數 是(復)規矩數若且唯若點 是 中的一個點。所有復規矩數構成的集合 也包含作為子集,並且是複數集的子集。從尺規可作性到解析幾何下的規矩數,尺規作圖問題從幾何問題轉成了代數的問題。
2.圓周率的超越性
 化圓為方
化圓為方 化圓為方
化圓為方化圓為方問題是指已知單位長度1,要作出 的長度。這等價於從1開始作出 。然而,能夠用尺規作出的數z都有對應的最小多項式。也就是說,存在有理係數的多項式m,使得
 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方然而,1882年,林德曼等人證明了對於圓周率 來說,這樣的多項式不存在。數學家將這樣的數稱為超越數,而將有對應的多項式的數稱為代數數。所有規矩數都是代數數,而 不是,這說明用尺規作圖是無法化圓為方的。
 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方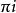 化圓為方
化圓為方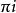 化圓為方
化圓為方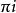 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方 化圓為方
化圓為方林德曼證明 的超越性用到了現在稱為林德曼-魏爾斯特拉斯定理的結論。林德曼-魏爾斯特拉斯定理說明,如果若干個代數數 在有理數域 上線性獨立,那么 也在 上線性獨立。反設 是代數數,那么 也是代數數。考慮代數數0和 ,由於 是無理數,所以它們在 上線性獨立。然而 和 分別是1和-1,並非在 上線性獨立,矛盾。這說明 不是代數數,而是超越數 。

