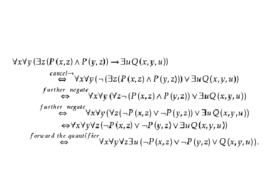前束範式

前束範式（prenex normal form）是數理邏輯中使用謂詞邏輯所描述的形式語言的一種格式。 前束範式亦稱前束式，一種謂詞演算公式。指其一切量詞都未被否定地處於公式的最前端且其轄域都延伸至公式的末端的謂詞演算公式。設Q∈∃，ᗄ，一個公式α是前束範式，若且唯若存在一個不含量詞的公式β，使得 α=(Q₁x₁)(Q₂x₂)…(Qₑxₑ)β. 例如，公式(ᗄx)[F(x)→G(x)]為一個前束範式，而(ᗄx)[F(x)∨G(x)]→(∃y)R(y)不是前束範式，與一個謂詞演算公式等價的前束範式公式稱為謂詞演算公式的前束範式，例如，公式p→(ᗄx)α(x)的前束範式為(ᗄx)[p→α(x)]，此處p為一個命題變元，其所有存在量詞都在全稱量詞的前面出現的前束範式稱為斯科朗範式，又稱∃前束範式，一個公式α是斯科朗範式，若且唯若存在一個不含量詞的公式β，使得 α=(∃x₁)(∃x₃)…(∃xₐ)(ᗄx₁) ·(ᗄx₂)…(ᗄxₑ)β(a≥0,e≥0).

定義

一個公式，如果量詞均在全式的開頭，它們的作用域延伸到整個公式的末端，則該公式叫做 前束範式(Prenex Normal Form)。

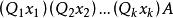前束範式

前束範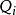式

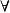前束範式

前束範式

前束範式

前束範式可記為下述形式 ，其中 為 或 ， 為個體變元，A是沒有量詞的謂詞公式。

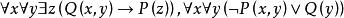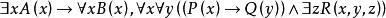前束範式

前束範式

例如， 等都是前束範式，而 等都不是前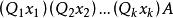束範式。

前束範式

定義 設P是具有形式 的前束範式，若A是合取範式，則稱P為 前束合取範式；若A是析取範式，則稱P為 前束析取範式。

利用換名規則、代替規則、量詞的否定公式及量詞轄域的擴張與收縮公式等，可以將任一謂詞公式化成前束範式。

定理

任何一個謂詞公式，均和一個前束範式等價。

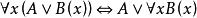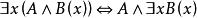前束範式

前束範式

證明 首先利用量詞轉化公式，把否定深入到命題變元和謂詞填式的前面，其次，利用 和 把量詞移到全式的最前面，這樣便得到前束範式。

求前束範式的過程

求一個謂詞公式的前束範式的過程為：

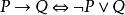前束範式

前束範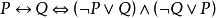式

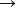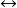前束範式

前束範式

(1)通過利用公式 及 消去渭詞公式中的聯結詞 和 ；

前束範式

(2)消去 ；

(3)否定深入，即利用量詞轉化公式把否定聯結詞深入到命題變元和謂詞填式的前面；

(4)運用換名規則和代替規則，將公式中所有變元均用不同的符號；

(5)量詞前移，即利用量詞轄域的擴張把量詞移到前面。

例題解析

求下列公式的前束範式：

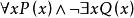前束範式

（1）

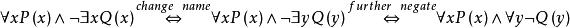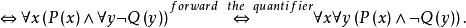前束範式

前束範式

或者

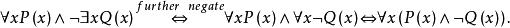前束範式

從（1）中可以看出一個公式的前束範式不是唯一的。

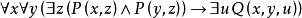前束範式

（2）

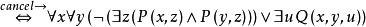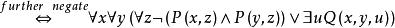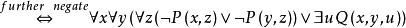前束範式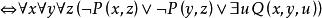

前束範式

前束範式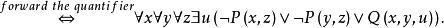

前束範式

前束範式