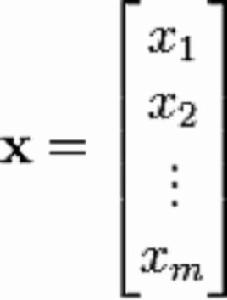向量
在數學中,向量(也稱為歐幾里得向量、幾何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示為帶箭頭的線段。箭頭所指:代表向量的方向;線段長度:代表向量的大小。與向量對應的只有大小,沒有方向的量叫做數量(物理學中稱標量)。
向量的記法:印刷體記作粗體的字母(如a、b、u、v),書寫時在字母頂上加一小箭頭“→”。 如果給定向量的起點(A)和終點(B),可將向量記作AB(並於頂上加→)。在空間直角坐標系中,也能把向量以數對形式表示,例如Oxy平面中(2,3)是一向量。
在物理學和工程學中,幾何向量更常被稱為矢量。許多物理量都是矢量,比如一個物體的位移,球撞向牆而對其施加的力等等。與之相對的是標量,即只有大小而沒有方向的量。一些與向量有關的定義亦與物理概念有密切的聯繫,例如向量勢對應於物理中的勢能。
幾何向量的概念線上性代數中經由抽象化,得到更一般的向量概念。此處向量定義為向量空間的元素,要注意這些抽象意義上的向量不一定以數對表示,大小和方向的概念亦不一定適用。因此,平日閱讀時需按照語境來區分文中所說的"向量"是哪一種概念。不過,依然可以找出一個向量空間的基來設定坐標系,也可以透過選取恰當的定義,在向量空間上介定範數和內積,這允許我們把抽象意義上的向量類比為具體的幾何向量。
簡介
列向量線上性代數中,列向量(Column vector)是一 m× 1的矩陣,即矩陣由一個包含 m個元素的列組成。
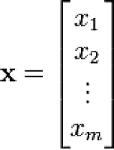 列向量
列向量為簡化書寫、方便排版起見,有時會以加上轉置符號T的行向量表示列向量。
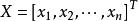 列向量
列向量為進一步化簡,習慣上會把行向量和列向量都寫成行的形式。不過行向量的元素是用空格或逗號隔開,列向量則用分號隔開。
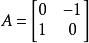 列向量
列向量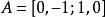 列向量
列向量例如為兩行兩列的矩陣,可寫為。
單位列向量
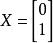 列向量
列向量單位列向量,即向量的長度為1,其向量所有元素的平方和為1。例如,就是一個單位列向量。
反之,若||x||=1,則X稱為單位向量。
||X||表示n維向量X長度(或範數)。
行向量
線上性代數中,行向量是一個 1× n的矩陣,即矩陣由一個含有 n個元素的行所組成即行向量。
行向量的轉置是一個列向量,反之亦然。
所有的行向量的集合形成一個向量空間,它是所有列向量集合的對偶空間。