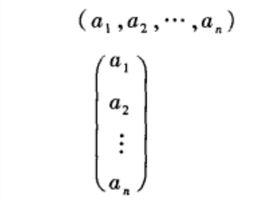基本介紹
n元向量亦稱n維向量，是普通平面和空間向量概念的推廣，是一種特殊的矩陣，數域P中的n個數的有序數組(a，a，…，a)，a(i=1，2，…，n)稱為這個向量的分量或坐標，P上全體n元向量構成的集合記為P ，P 中兩個n元向量相等是指它們的對應分量完全相同 。根據需要，一個n元向量(a，a，…，a)也可以表示為
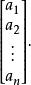n元向量並稱前者為行向量，後者為列向量 。
n元向量常用希臘字母α，β，γ等表示。
n元向量的運算
n元向量的加法，P中的數與n元向量的數量乘法(簡稱數乘)定義為：
(a，a，…，a)+(b，b，…，b)=(a+b，a+b，…，a+b)；
c(a，a，…，a)=(ca，ca，…，ca) (c∈P).
分量都是0的n元向量(0，0，…，0)稱為零向量，記為0；將n元向量α的各分量變號後所得到的向量，稱為α的負向量，記為-α；P的全體n元向量滿足線性空間的全部運算規律，構成數域P上的一個線性空間，稱為P上的 n維向量空間，亦稱n維矢量空間。除了以上兩種運算，n元向量還符合加法交換律，加法結合律等 。
n元單位向量
稱n元向量
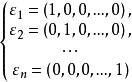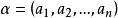n元向量
n元向量為單位向量。顯然，對任意n元向量都有
n元向量即任意向量都可由單位向量線性表示，而且這種表示方法還是唯一的 。
n元向量的相等
兩個n元向量
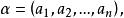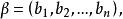n元向量
n元向量若且唯若它們的對應分量相等，即
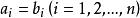n元向量時，認為是相等的，記作
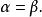n元向量