定義
向量空間的基本模型是n維行向量或列向量的空間:
 實向量空間
實向量空間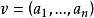 實向量空間
實向量空間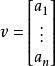 實向量空間
實向量空間:行向量的集合,或列向量的集合。
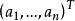 實向量空間
實向量空間雖然行向量寫起來占的空間較少,但矩陣乘法的定義使得列向量對我們更方便。因而多數情況下使用列向量,為了節省空間,我們有時把列向量寫成的形式。
向量加法:
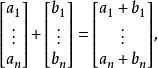 實向量空間
實向量空間標量乘法:
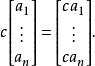 實向量空間
實向量空間 實向量空間
實向量空間這些運算使成為一個向量空間。
 實向量空間
實向量空間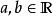 實向量空間
實向量空間 實向量空間
實向量空間一個 實向量空間是具有兩個合成法則的集合(所有及所有):
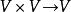 實向量空間
實向量空間(a) 向量加法:;
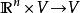 實向量空間
實向量空間(b) 標量乘法:;
並且這兩個合成法則必須滿足下列公理:
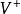 實向量空間
實向量空間(i)加法使V成為阿貝爾群;
(ii)標量乘法與實數乘法是結合的:
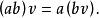 實向量空間
實向量空間(iii)用實數1作標量乘法是恆等作用:
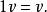 實向量空間
實向量空間(iv)兩個分配律成立:
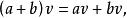 實向量空間
實向量空間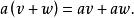 實向量空間
實向量空間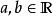 實向量空間
實向量空間 實向量空間
實向量空間當然,所有公理都應加上全稱量詞,即假設它們對所有及所有。
 實向量空間
實向量空間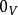 實向量空間
實向量空間中加法的單位元記作0,或者,為了不混淆零向量和 數0,記作。
 實向量空間
實向量空間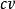 實向量空間
實向量空間注意,標量乘法將由實數c和向量組成的每對元素對應另一向量,這樣的法則稱為向量空間的外部合成法則。
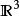 實向量空間
實向量空間兩個向量的乘法不是結構的一部分,雖然可以定義不同的積,如中向量的叉積,這些積不完全是內在的,它們依賴於坐標的選擇,因此將它們看成向量空間上的額外結構。
仔細看一下公理(ii).左邊是指先把a和b作為實數相乘,然後用ab和v作標量乘法而得到的向量,右邊兩個運算都是標量乘法。
兩個合成法則由基本的分配律聯繫起來.注意,在第一個分配律中左邊的符號+代表實數加法,而在右邊則代表向量加法。
相關性質
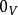 實向量空間
實向量空間在一個向量空間V中,下列等式成立(零向量記作):
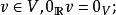 實向量空間
實向量空間(a)對所有
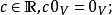 實向量空間
實向量空間(b)對所有
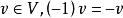 實向量空間
實向量空間(c)對所有.
證明 為證(a),用分配律寫出
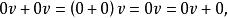 實向量空間
實向量空間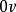 實向量空間
實向量空間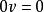 實向量空間
實向量空間兩邊消去得到。請仔細看一下,注意哪個0是數,哪個0是向量。
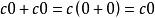 實向量空間
實向量空間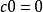 實向量空間
實向量空間類似地,。於是。最後
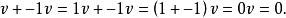 實向量空間
實向量空間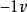 實向量空間
實向量空間 實向量空間
實向量空間因而,是的加法逆。
 實向量空間
實向量空間 實向量空間
實向量空間例1的子空間是一個這樣的向量空間,即它的合成法則由上的合成法則導出。
 實向量空間
實向量空間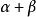 實向量空間
實向量空間 實向量空間
實向量空間 實向量空間
實向量空間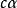 實向量空間
實向量空間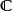 實向量空間
實向量空間例2 設是複數集.忘掉複數乘法,只保持加法以及複數和實數的乘法,這使得成為實向量空間。
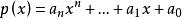 實向量空間
實向量空間例3 實多項式的集合是向量空間,其合成法則為多項式的加法以及標量和多項式的乘法。
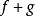 實向量空間
實向量空間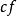 實向量空間
實向量空間例4 設V是區間[0,1]上實值連續函式的集合,只看函式加法以及數與函式的乘法兩個運算,這使得V成為實向量空間。
注意,這些例子都有比我們將其視為向量空間更多的結構,這些是很典型的例子,每一個例子一定有不同於其他例子的特性,這並不是定義的缺陷,恰好相反,抽象方法的威力就在於一般公理的結論可用於許多不同的實例。