基本介紹
行向量、列向量 若 A為一m×n矩陣, A的每一行為一個實的n元組,於是可將其看成是 R 中的一個向量。對應於 A的m個行的向量稱為 A的 行向量(row vector)。類似地, A的每一列可以看成是 R 中的一個向量,且稱這n個向量為 A的 列向量(column vector)。
行空間、列空間 如果 A為一m×n矩陣,由 A的行向量張成的 R 的子空間稱為 A的 行空 間(row space)。由 A的各列張成的 R 的子空間稱為 A的 列空間(column space)。
例1 令
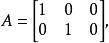 列空間
列空間A的行空間是所有如下形式的3元組:
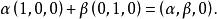 列空間
列空間A的列空間是所有如下形式的向量:
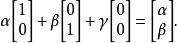 列空間
列空間因此, A的行空間為一個 R 的二維子空間,且 A的列空間為 R。
列空間與線性方程組
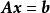 列空間
列空間在研究線性方程組時,行空間和列空間的概念十分有用,一個方程組可寫為
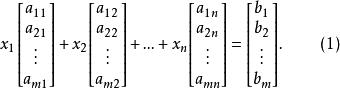 列空間
列空間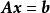 列空間
列空間 列空間
列空間定理1(線性方程組的相容性定理) 一個線性方程組相容的充要條件是 b在的列空間中。
若將 b用零向量替代,則(1)化為
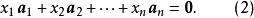 列空間
列空間 列空間
列空間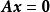 列空間
列空間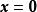 列空間
列空間由(2)知,若且唯若的列向量線性無關時,方程組僅有平凡解。
 列空間
列空間 列空間
列空間 列空間
列空間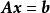 列空間
列空間 列空間
列空間 列空間
列空間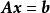 列空間
列空間定理2 令為一m×n矩陣, 若且唯若的列向量張成 R 時,對每一,線性方程組是相容的,若且唯若的列向量線性無關時,對每一,方程組至多有一個解。
 列空間
列空間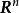 列空間
列空間 列空間
列空間推論 若且唯若一個n×n矩陣的列向量為的一組基時,是非奇異的。
一般地,矩陣的秩和其零空間的維數加起來等於矩陣的列數。一個矩陣的零空間的維數稱為矩陣的零度(nullity)。
 列空間
列空間 列空間
列空間 列空間
列空間定理3(秩一零度定理) 若為一m×n矩陣,則的秩與的零度的和為n 。
相關定理
定理4 兩個行等價的矩陣有相同的行空間。
證明: 若 B行等價於 A,則 B可由 A經有限次行運算得到。因此, B的行向量必為 A的行向量的線性組合。所以, B的行空間必為 A的行空間的子空間,因為 A行等價於 B,由相同的原因, A的行空間是 B的行空間的子空間。
定義 A的行空間的維數稱為矩陣 A的秩(rank)。
為求矩陣的秩,可以將矩陣化為行階梯形矩陣,行階梯形矩陣中的非零行將構成行空間的一組基。
例2令
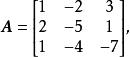 列空間
列空間將 A 化為行階梯形,得到矩陣
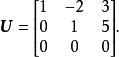 列空間
列空間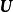 列空間
列空間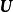 列空間
列空間顯然,(1,-2,,3)和(0,1,5)構成的行空間的一組基。因為和 A是行等價所以它們有相同的行空間,且因此 A 的秩為2。
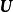 列空間
列空間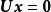 列空間
列空間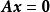 列空間
列空間一般地,若 A為一m×n矩陣,且是 A的行階梯形,則由於若且唯若時,,故它們的列向量滿足相同的依賴關係。
定理5若 A為一m×n矩陣,則 A的行空間的維數等於 A的列空間的維數 。
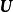 列空間
列空間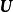 列空間
列空間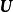 列空間
列空間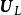 列空間
列空間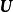 列空間
列空間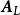 列空間
列空間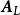 列空間
列空間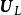 列空間
列空間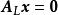 列空間
列空間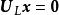 列空間
列空間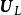 列空間
列空間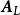 列空間
列空間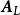 列空間
列空間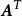 列空間
列空間證明: 若 A為一秩為r的m×n矩陣,則 A的行階梯形將有r個首1元素。中對應於首1元素的列將是線性無關的。然而,它們並不構成 A的列空間的基,這是因為,一般地, A和有不同的列空間。令為消去中自由變數所在的列得到的新矩陣。從 A中消去相應的列,並記新矩陣為。矩陣和也是行等價的。因此,若 x為的一個解,則 x必為的解。因為的各列是線性無關的,故 x必為 0,因此,的各列也是線性無關的,因為有r列,所以 A的列空間的維數至少為r。因為對任何矩陣,其列空間的維數大於或等於行空間的維數,將這個結論套用於,我們有
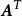 列空間
列空間dim( A的行空間)=dim(的列空間)
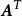 列空間
列空間≥dim(的行空間)
=dim( A的列空間)
因此,對任何矩陣 A,行空間的維數必等於列空間的維數。
 列空間
列空間 列空間
列空間我們可以利用 A的行階梯形求 A的列空間的一組基。我們只需求中對應於首1元素的列即可。 A中的相應列將是線性無關的,並構成 A的列空間的一組基。
 列空間
列空間 列空間
列空間 列空間
列空間注意: 行階梯形僅告訴我們 A的哪一列用於構成基。但不能用的列作為基向量,這是因為和 A一般有不同的列空間。