概述
在計算複雜度理論中，分團問題(clique problem)是圖論中的一個NP完備(NP-complete)問題。
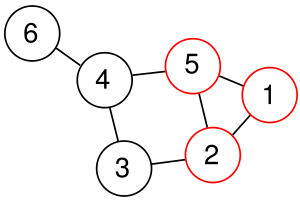
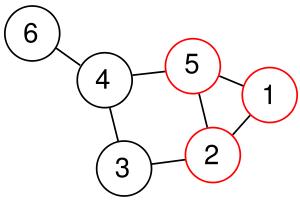圖1.一個大小為3的clique一個大小為3的clique，clique是一個圖中兩兩相連的一個點集，或是一個完全子圖(complete subgraph)，如右圖中的1, 2, 5三個點。
clique problem是問一個圖中是否有大小是k以上的clique。任意挑出k個點，我們可以簡單的判斷出這k個點是不是一個clique，所以這個問題屬於NP。
證明clique problem是NP完備可以很簡單的從獨立頂點集問題（Independent set problem）reduce。因為存在一個大小是k以上的clique等價於它的complement graph中存在一個大小是k以上的Independent set。
算法
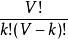分團問題最簡單的方法是用暴力法列舉圖中所有 k個點的子集合，並檢查它是不是clique。在一個有 V個點的圖中用暴力法找大小是 k的clique至少要檢查 個子集合。
另外一個啟發式的方法是先找出所有一個點的clique，再慢慢合併成更大的clique直到不能再合併為止。
參見
•計算複雜性理論
•數學問題
