簡介
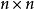冪零矩陣
冪零矩陣
冪零矩陣線上性代數中，對於的方陣N，存在正整數k，使得，這樣的方陣N就叫做冪零矩陣。滿足條件的最小的正整數k被稱為N的度數或指數。更一般來說，零權變換是向量空間的線性變換L，使得對於一些正整數k（並且因此，對於所有j≥k，Lj = 0），。
冪零矩陣是冪零元──一個更加一般的概念的特殊情況，不僅可以套用於矩陣和線性變換，也可以套用於環的元素。
性質
對於具有真實（或複雜）元素的n×n個方陣N，以下是等價的：
（1）N是冪零矩陣。
冪零矩陣（2）對於一些正整數k≤n，N的最小多項式為。
冪零矩陣（3）N的特徵多項式為。
（4）N的唯一特徵值為0。
冪零矩陣（5）對於所有k> 0，tr（）= 0。
最後一個定理適用於特徵值為0或特徵值足夠大的矩陣。 （參考牛頓的證實）
這個定理有幾個結論，包括：
（1）n×n冪零矩陣的度數總是小於或等於n。
（2）冪零矩陣不是可逆矩陣的。
（3）唯一冪零且可對角化的矩陣是零矩陣。
（4）若M為實對稱矩陣，則M=0。
（5）非零的冪零矩陣A不能對角化。
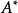冪零矩陣
冪零矩陣（6）若A為n階冪零矩陣，則，均為冪零陣。
舉例
冪零矩陣
冪零矩陣矩陣M=是冪零矩陣，因為。
冪零矩陣更一般地說，主對角線均為0的任何三角矩陣均為冪零矩陣，指數。 例如，矩陣
冪零矩陣
冪零矩陣是冪零矩陣，因為。
雖然上面的例子中的矩陣有大量的0元素，但是一個典型的冪零矩陣可能沒有0元素。 例如，矩陣
冪零矩陣，儘管矩陣沒有零項，但是其冪次方為零矩陣，因此該矩陣為冪零矩陣。
分類
考慮n×n階移位矩陣：
冪零矩陣
冪零矩陣該矩陣沿著超對角線有若干個元素1，其他地方均為元素0。 作為線性變換，移位矩陣將矢量的分量向左移動一個位置，零出現在最後位置：。
該矩陣是度為零，並且是“規範””的冪零矩陣。
具體地說，如果N是任何非零矩陣，則N與下面形式的分塊對角矩陣相似。
冪零矩陣其中塊S1，S2，...，Sr中的每一個是移位矩陣（可能具有不同大小）。這種形式是規範冪零矩陣形式的特殊情況。
附加屬性
如果N是冪零矩陣，則I + N是可逆的，其中I是n×n個單位矩陣。 逆矩陣如下，
冪零矩陣其中有限條件為總和是非零的。
冪零矩陣
冪零矩陣如果N是冪零矩陣，，其中I表示n×n單位矩陣。 相反，如果存在矩陣A，若等式對於t的所有值均成立，則A是冪零矩陣。
每個奇異矩陣都可以寫成一個冪零矩陣的乘積。
冪零矩陣是收斂矩陣的一種特殊情況。
