定義
不可約矩陣和可約矩陣（reducible matrix）兩個相對的概念。
表述一
不可約矩陣
不可約矩陣
不可約矩陣
不可約矩陣
不可約矩陣
不可約矩陣 不可約矩陣設 ，若存在置換矩陣 ，使得 ，其中 是階數不小於1的方陣， 是零矩陣，則稱 是可約的；否則稱矩陣 是不可約的。
表述二
不可約矩陣
不可約矩陣
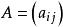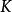不可約矩陣
不可約矩陣
不可約矩陣
不可約矩陣
不可約矩陣 不可約矩陣 不可約矩陣對於 階方陣 而言，如果指標集 {1，2，...，n} 能夠被劃分成兩個不相交的非空指標集 和 ，使得對任意的 和任意的 都有 ，則稱矩陣 是可約的；否則稱矩陣 是不可約的。
可約矩陣
不可約矩陣其中A矩陣其對應的有向圖並非強連通，故這個矩陣是可約的，其對應有向圖如下所示：
不可約矩陣不可約矩陣
不可約矩陣相關定理
定理1
不可約矩陣 不可約矩陣 不可約矩陣
不可約矩陣階複數方陣 是不可約的若且唯若與矩陣 對應的有向圖 是強連通的。
不可約矩陣
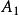不可約矩陣 不可約矩陣
不可約矩陣
不可約矩陣說明：不可約矩陣不能分解成 的形式，其中 為方陣， 為零矩陣。該定理的證明是顯然的，不可約矩陣的么的任意次冪總是不可約的，因此它的右上角有一個零塊。這個零塊表明在 所對應的頂點與 所對應的頂點之間無通路。反之，如果一個有向圖不是強連通的，則有一個不可達的頂點所對應的子塊，經過適當的置換之後，對應的矩陣可以化為上面提到的形式。
定理2
不可約矩陣一個方陣 或者是不可約的，或者可以通過置換化為這樣的規範形式：
不可約矩陣式中對角線上的子塊是不可約陣。矩陣中出現對下標子塊的任意一行至少有一個非零子塊。
說明：為證明這一定理，假定矩陣是可約的，因而它可以表示為可約矩陣定義的那種形式。如果對角線上的予塊仍是可約的，這些子塊又可以表示為那種定義形式。因此，只要對角線上的子塊是可約的，總可表示為定義形式。經過適當地置換之後，主對角線上方的子塊全部為零，對角線上的子塊是不可約的。然後對於主對角線上的子塊是唯一非零子塊的那些行進行適當置換即可得到上述規範形式。
不可約矩陣
不可約矩陣
不可約矩陣注意到在圖論的意義上，每個孤立的子塊從雙下標所對應的結點是可達的，反之則不然。上述矩陣中每一列的所有雙下標子陣可以簡單寫成一行子塊，這裡不再是不可約的。若不考慮子塊指標的置換，這種形式是唯一的。
不可約矩陣最後我們考慮矩陣的轉置，子塊構成矩陣的最後一列。事實上這是我們以後要用到的一種形式，即所謂排序的隨機矩陣。排序的隨機矩陣正規形式的構造可先從任意一個元素開始，在它所在的列中填寫對這個元素有影響作用的所有元素的排序權值（即特徵向量的分量）。然後再進行下一列，直到對這組元素全部填寫完畢為止，必須逐元素地進行填寫工作。對每一個不可約子集可得一個子塊，填寫完一塊之後再填寫下一塊。
定理3
不可約矩陣
不可約矩陣（1）若且唯若不可約時，是不可約的；
不可約矩陣
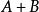不可約矩陣
不可約矩陣（2）若是不可約的非負矩陣，為非負矩陣，則是不可約矩陣。
證明：
對（1）是顯然成立的。
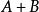不可約矩陣 不可約矩陣對（2）採取反證法。若是可約的，則存在置換矩陣使得：
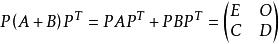不可約矩陣
不可約矩陣
不可約矩陣 不可約矩陣由於都是非負矩陣，故都必須具有上式右端的形式，這與是不可約的相互矛盾。
