介紹
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣多項式矩陣即元為多項式的矩陣。 為 矩陣,或多項式矩陣,其中 是 的多項式。多項式矩陣,也稱為λ-矩陣、矩陣係數多項式(不是矩陣多項式),是數學中矩陣論里的概念,指係數是多項式的方塊矩陣。使用“λ-矩陣”的名稱時,說明係數多項式以λ為不定元。
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣若n階多項式矩陣 的行列式 (非零多項式),則稱 是滿秩的(秩=n)或非奇異的。
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣若使 ,則稱 是可逆的,或稱 是單模矩陣,記為 。
多項式矩陣
運算註解
多項式矩陣的加法、數乘、及乘法與一般矩陣的運算規則一樣,只是在運算過程中將式的運算換成多項式的運算即可。
多項式矩陣也像數字矩陣那樣定義行列式,並且多項式矩陣行列式的性質與數字矩陣行列式的性質相同。
初等變換
①互換的任意兩行(列)
②以非零數c乘以矩陣的一行(列)
 多項式矩陣
多項式矩陣③矩陣的某一行(列)乘以多項式 )後某一行加到另一行(列)
多項式矩陣的秩
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣如果多項式矩陣 有一個r階子式不為零,而所有的r+1階子式全為零,則稱 的秩為r,零矩陣的秩規定為0。
多項式矩陣的逆矩陣
 多項式矩陣
多項式矩陣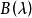 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣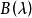 多項式矩陣
多項式矩陣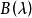 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣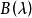 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣設 為n階λ-矩陣,如果存在n階λ-矩陣 ,使 = =l,則稱 可逆,並稱 為 的逆矩陣。
多項式矩陣的等價
 多項式矩陣
多項式矩陣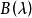 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣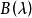 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣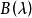 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣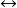 多項式矩陣
多項式矩陣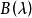 多項式矩陣
多項式矩陣設 、 ,如果有 經過有限次初等變換能變為 ,則稱多項式矩陣 稱為與 等價,記為 。
多項式矩陣的行列式因子
1、定義
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣設 矩陣的秩為r,對於正整數k, , 中必有非零的k級子式, 中全部k級子式的首項係數為1的最大公因式 稱為 的k階行列式因子。
 多項式矩陣
多項式矩陣2、不變因子
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣中所有因子稱為 的不變因子組。
 多項式矩陣
多項式矩陣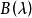 多項式矩陣
多項式矩陣經過初等變換不改變多項式矩陣的秩和行列式因子,有相同的行列式因子或不變因子是 與等價的充要條件。
3、初等因子
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣設矩陣的不變因子為的標準分解式是
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣則稱的標準分解式中的一次因式的方冪為A的初等因子。A中所有的初等因子稱為A的初等因子組。由定義知,初等因子是由不變因子確定的。
多項式矩陣的標準型
1、Smith標準形
 多項式矩陣
多項式矩陣對任一非零多項式矩陣 ,都等價於下列形式的矩陣(經過矩陣的初等變換實現):
 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣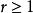 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣 多項式矩陣
多項式矩陣則稱它是 的更密斯(Smith)標準形,其中是它的秩,是首項係數為1的多項式,且。其中主對角線上的非零元素稱為 的不變因子。
2、Jordan標準形
形如
 多項式矩陣
多項式矩陣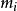 多項式矩陣
多項式矩陣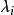 多項式矩陣
多項式矩陣的方陣稱為階Jordan塊,其中可以是實數,也可以是複數。
套用
1、矩陣理論在計算機方面的套用,如矩陣的奇異值分解的套用,QR分解在網路方面的套用,還有在三維圖形圖像方面的套用。
2、多項式矩陣理論在網路分析中的套用,基於迴路矩陣B、基本割集矩陣Q和支路伏安特矩陣,藉助多項式理論中有關解耦零點的概念和理論,研究網路的複雜度和穩定性。
3、多項式矩陣理論知識,在建立和完善線性控制系統理論過程中具有基礎作用,套用廣泛。
